Системы случайных величин
Существенный интерес в математической статистике представляет рассмотрение системы двух и более случайных величин и их статистическая взаимосвязь друг с другом.
По аналогии с рядом распределения одной дискретной величины
Х
для двух дискретных случайных величин
X
и
Y
строится
матрица распределения
– прямоугольная таблица, в которой записаны все вероятности
p
i j
=
P
{
X = x
i
,
Y = y
j
} ,
i
= 1, … ,
n
;
j
= 1,…,
m
.
События (или опыты) называются
независимыми
, если вероятность появления (исхода) каждого из них не зависит от того, какие события (исходы) имели место в других случаях (опытах).
Две случайные величины
X
и
Y
называются
независимыми
, если независимы все связанные с ними события: например, {
X
<
а
} и {
Y
<
b
} или {
X
=
x
i
} и {
Y
=
y
i
} и т.д.
В терминах законов распределения справедливо также следующее определение: две случайные величины
X
и
Y
называются
независимыми
, если закон распределения каждой из них не зависит от принятого значения другой.
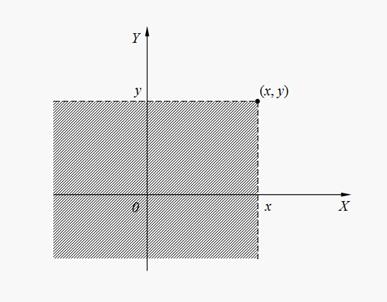
Совместной функцией распределения системы двух случайных величин ( X , Y ) называется вероятность совместного выполнения неравенств X < х и Y < у :
Событие
Рис. 8. Геометрическая интерпретация совместной функции распределения F ( x , y )
Здесь
называется совместной плотностью распределения системы двух случайных величин ( X , Y ). Основные свойства совместной плотности распределения:
В качестве числовых характеристик системы двух случайных величин
X
и
Y
обычно рассматриваются
начальные
и
центральные моменты
различных порядков.
Порядком момента
называется сумма его индексов
k
+
s
.
Начальным моментом порядка k + s системы двух случайных величин X и Y называется математическое ожидание произведения X k на Y s :
Центральным моментом порядка k + s системы двух случайных величин ( X , Y ) называется математическое ожидание произведения ( X – m x ) k на ( Y – m y ) s :
где m x = М ( Х ), m y = М ( Y ). Для системы дискретных случайных величин X и Y :
где р i j = Р { Х = x i , Y = y j }.
где
f
(
x
,
y
) – совместная плотность распределения случайных величин
X
и
Y
.
В инженерных приложениях математической статистики чаще всего используются моменты первого и второго порядков. Начальные моменты первого порядка
являются математическими ожиданиями случайных величин X и Y . Центральные моменты первого порядка всегда равны нулю:
Центральные моменты второго порядка:
Здесь D x , D y – дисперсии случайных величин X и Y .
Центральный момент второго порядка
Из определения ковариации (48) следует:
По определению ковариации (48) получим:
Ковариация двух случайных величин
X
и
Y
характеризует степень их зависимости и меру рассеивания вокруг точки
Выражение (52) вытекает из определения ковариации (48).
Размерность ковариации
Безразмерная величина, характеризующая только зависимость случайных величин X и Y , а не разброс:
называется коэффициентом корреляции случайных величин X и Y . Этот параметр характеризует степень линейной зависимости случайных
величин
X
и
Y
. Для любых двух случайных величин
X
и
Y
коэффициент корреляции
|
Содержание
>> Прикладная математика
>> Математическая статистика
>> Элементы математической статистики
>> Системы случайных величин
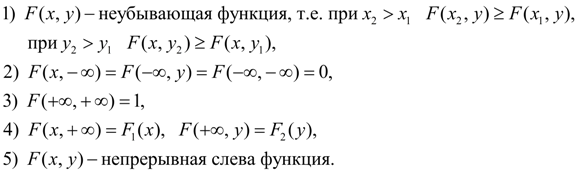 (35)
(35)
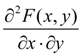 . Обе случайные величины
X
и
Y
– непрерывны. Тогда функция
. Обе случайные величины
X
и
Y
– непрерывны. Тогда функция
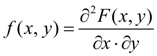 (36)
(36)
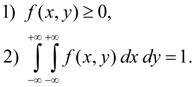 (37)
(37)
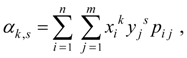 (40)
(40)
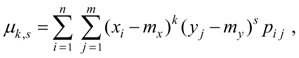 (41)
(41)
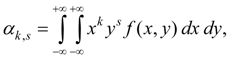 (42)
(42)
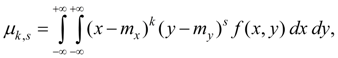 (43)
(43)
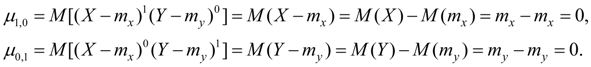 (45)
(45)
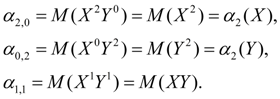 (46)
(46)
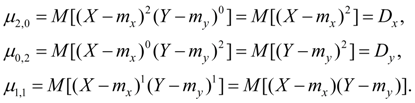 (47)
(47)
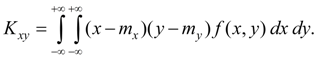 (51)
(51)
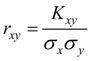 (53)
(53)