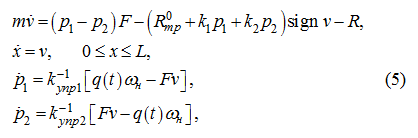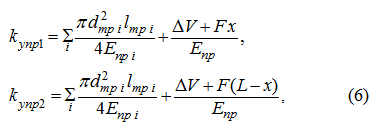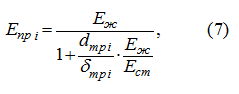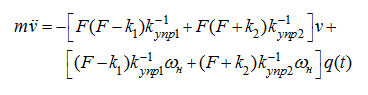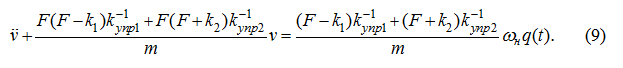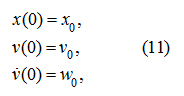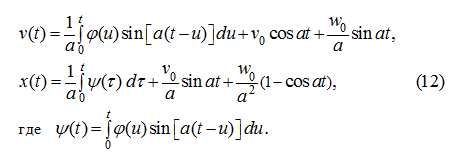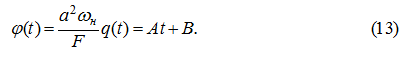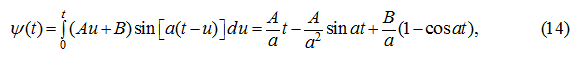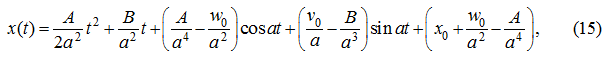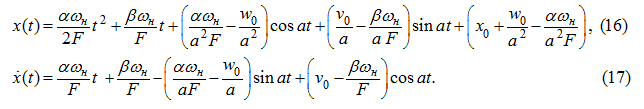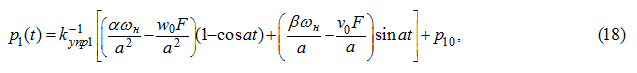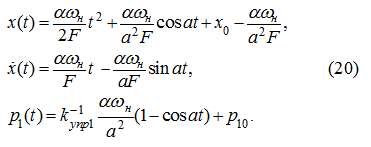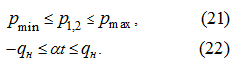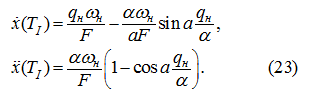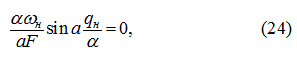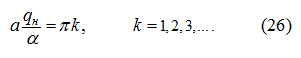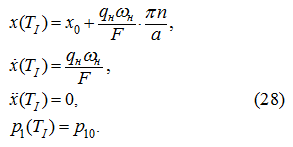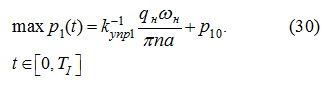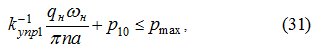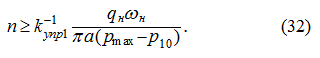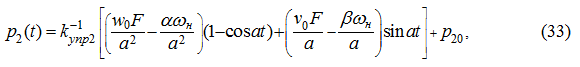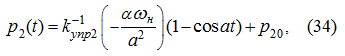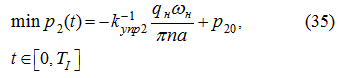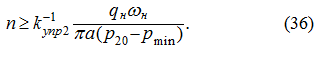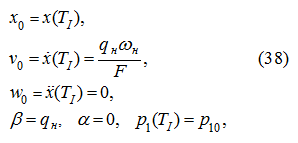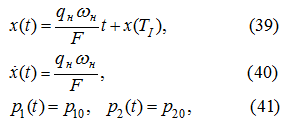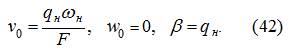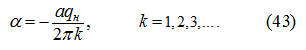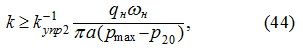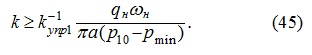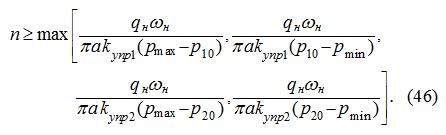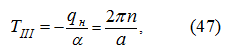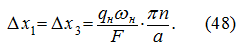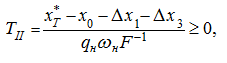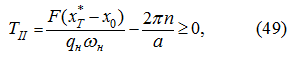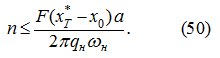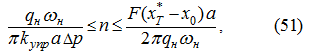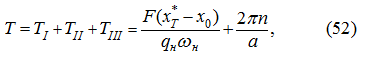|
Системы управления - Динамический синтез - Метод кратных периодов собственных колебаний - Алгоритм
Алгоритм
Рассмотрим упрощенную расчетную схему гидропривода поступательного движения с замкнутой циркуляцией потока (рис. 3).
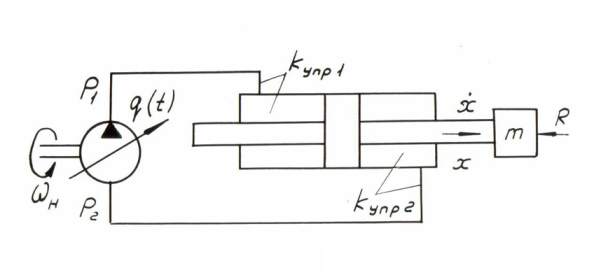
Рис. 3.
Запишем систему дифференциальных уравнений динамики рассматриваемой гидросхемы с учетом упругости рабочей жидкости, приняв следующие
допущения:
1) утечки рабочей жидкости в гидросистеме отсутствуют, поэтому работа системы подпитки не рассматривается;
2) потери давления по длине трубопроводов и в местных сопротивлениях пренебрежимо малы;
3) приведенные масса и нагрузка на штоке гидроцилиндра, а также частота вращения вала насоса постоянны;
4) параметры рабочей жидкости (плотность, вязкость, модуль объемной упругости) постоянны;
5) динамика механизма управления подачей насоса на данном этапе решения не рассматривается.
Учет динамики механизма управления подачей насоса не представляет принципиальных трудностей, так как эта задача может быть решена и
после (параллельно) рассматриваемой, когда искомая зависимость рабочего объема насоса
q
(
t
) (или хотя бы его
текущее численное значение) уже известна. Для этого следует записать математическую модель механизма управления, выходом которой
является
q
(
t
).
Математическая модель рассматриваемой гидросистемы с учетом принятых допущений имеет вид:
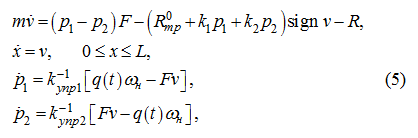
где
m
– приведенная к штоку масса подвижных частей исполнительного механизма;
р
1
,
р
2
– давления в напорной и сливной полостях гидросистемы;
x
,
v
– перемещение и скорость поршня гидроцилиндра;
R
0
тр
– постоянная сила сухого трения в уплотнениях гидроцилиндра при отсутствии давлений в
полостях;
k
1
,
k
2
– коэффициенты пропорциональности в переменных составляющих силы трения,
зависящих от давления;
R
– постоянная нагрузка на штоке гидроцилиндра;
ω
н
– угловая скорость вала насоса;
F
– рабочая площадь поршня гидроцилиндра;
q
(
t
) – рабочий объем насоса в функции времени (собственно сигнал
управления);
k
упр
1
,
k
упр
2
– коэффициенты упругости полостей гидросистемы,
равные:
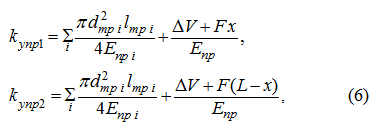
где
L
– максимальный ход поршня гидроцилиндра;
d
тр i
,
l
тр i
– диаметр и длина
i
-го трубопровода; Δ
V
–«мертвый» объем полости гидроцилиндра;
Е
пр i
– приведенный модуль
объемной упругости
i
-го трубопровода с рабочей жидкостью:
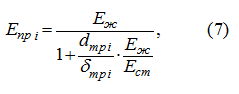
где
Е
ж
– модуль объемной упругости рабочей жидкости;
δ
тр i
– толщина стенки
i
-го
трубопровода;
Е
ст
– модуль упругости материала стенки трубопровода;
Е
пр
– приведенный модуль
упругости полости гидроцилиндра, определяемый аналогичным (7) образом.
Положим для простоты
v
> 0, то есть sign
v
= 1.
Дифференцируя по времени первое из уравнений системы (5), с учетом принятых допущений получим:
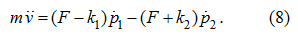
Подставляя в (8)
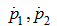 из последних двух уравнений системы (5), получим:
из последних двух уравнений системы (5), получим:
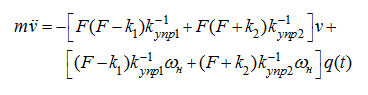
или
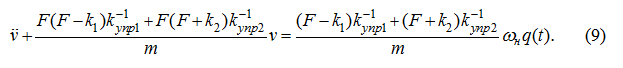
Несмотря на зависимость (6) коэффициентов упругости
k
упр
1
и
k
упр
2
от
х
, в рамках
принятых допущений и для реальных значений
F
,
k
1
,
k
2
и других параметров, нетрудно
показать (см.
Приложение
), что выражение, стоящее в
уравнении (9) в качестве множителя перед
v
, меняется незначительно (~13%), поэтому в первом приближении можно считать
уравнение (9) линейным:
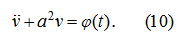
Задав начальные условия:
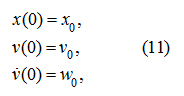
получим решение уравнения (10), которое с учетом начальных условий (11) имеет вид [9]:
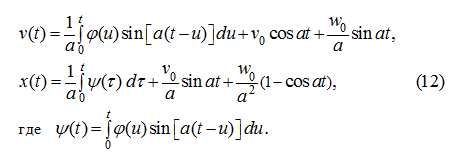
Исходя из условий точности позиционирования, необходимо выбрать управление
φ
(
t
) таким образом, чтобы к моменту
окончания регулирования погасить собственные колебания.
Рассмотрим класс линейных управлений
φ
(
t
) (в общем случае – кусочно-линейных, если учесть, что для каждого этапа
движения временной интервал (0,
t
) является «скользящим», то есть его левая граница соответствует
t
= 0; иными
словами, начальные условия (11) для 2-го и 3-го этапа движения заменяются значениями фазовых переменных в конце предыдущего этапа).
Итак, пусть
q
(
t
) =
α
t
+
β
, тогда
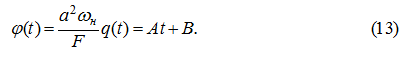
Подставляя (13) в (12), получим:
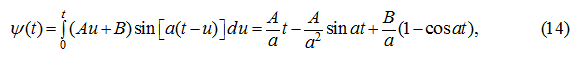
откуда
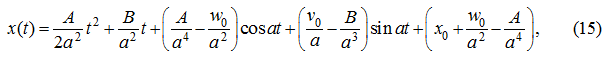
или окончательно:
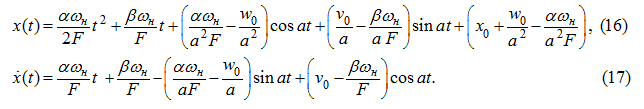
Подставляя (17) в уравнение (5) для
р
1
и интегрируя по
t
, получим:
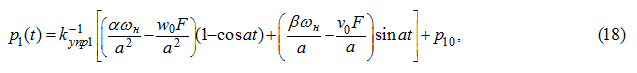
где
р
10
=
р
1
(0).
Рассмотрим отдельно основные фазы движения и управления.
Разгон
Начальные условия при разгоне:
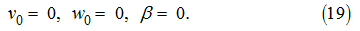
В этом случае имеем:
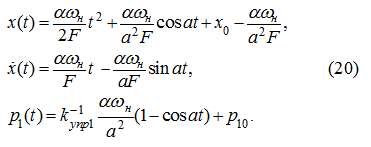
Введем ограничения:
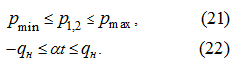
Первое из ограничений (21) вводится, исходя из требований эксплуатации гидросистемы, а именно: давление не должно быть ниже некоторого
минимального уровня, определяемого условиями всасывания рабочей жидкости на входе основного насоса и не должно достигать давления
срабатывания предохранительного клапана, так как в противном случае будет искажен желаемый процесс управления гидроприводом.
Ограничения (22) отражают чисто геометрические возможности регулируемого насоса.
Пусть
T
I
– время управления при разгоне, тогда
T
I
=
q
н
/
α
.
При
t
=
T
I
получим:
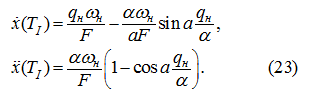
Потребуем, чтобы
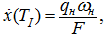 тогда:
тогда:
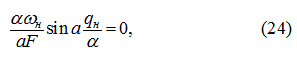
откуда

и
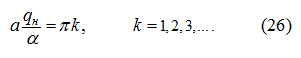
Если принять
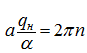 (для того, чтобы в конце разгона
(для того, чтобы в конце разгона
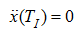 ),
то
),
то
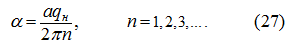
Тогда при
t
=
T
I
имеем:
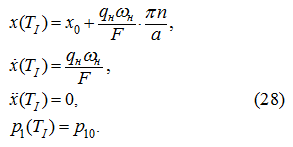
Найдем max
p
1
(
t
) при (27) на временнóм промежутке 0 ≤
t
≤
T
I
:
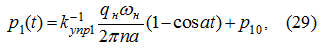
а так как
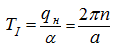 – период функции
p
1
(
t
), то ее максимум на [0,
T
I
] равен:
– период функции
p
1
(
t
), то ее максимум на [0,
T
I
] равен:
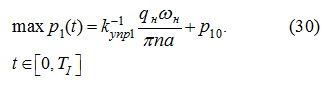
Из условия (21) получим:
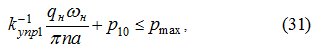
откуда следует:
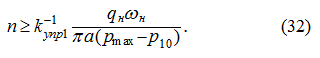
С другой стороны,
при отсутствии системы подпитки
давление
р
2
в сливной магистрали меняется аналогично (18):
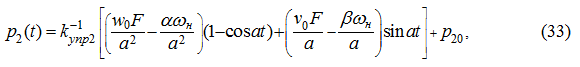
где
р
20
=
р
2
(0).
При разгоне, с учетом начальных условий (19), получим:
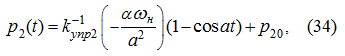
откуда исходя из ограничения (21) с учетом (27), получим:
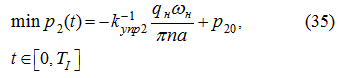
следовательно,
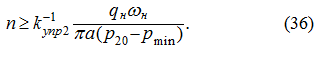
Таким образом, из (32) и (36) следует, что при разгоне:

Еще раз подчеркнем, что справедливость формул (34) – (37) имеет место
только при отсутствии системы подпитки.
При наличии
последней необходимость в этих условиях отпадает.
Установившееся движение
Для этого этапа движения задаются новые начальные условия:
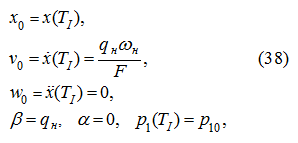
где
 – значения соответствующих фазовых координат в конце предыдущего этапа движения (разгона).
Подставляя (38) в уравнения (16), (17) и (18), соответственно получим:
– значения соответствующих фазовых координат в конце предыдущего этапа движения (разгона).
Подставляя (38) в уравнения (16), (17) и (18), соответственно получим:
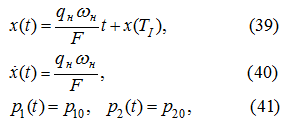
откуда очевидно, что на временнóм промежутке
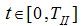 имеет место равномерное движение гидропривода. Величина
T
II
(длительность установившегося движения) будет
определена позже.
имеет место равномерное движение гидропривода. Величина
T
II
(длительность установившегося движения) будет
определена позже.
Торможение
Начальные условия на этапе торможения:
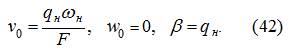
Если принять аналогично (27) при разгоне, что при торможении
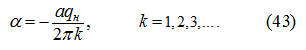
то подставляя (42) в уравнения (16), (17) и (18), получим из условия (21) аналогично предыдущему:
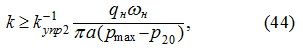
и
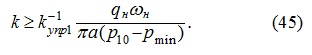
Если принять в качестве
n
и
k
их общие значения для всех режимов, то тогда
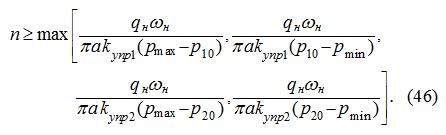
Длительность торможения в этом случае составит:
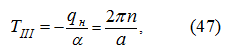
тогда перемещения поршня при разгоне Δ
х
1
и торможении Δ
х
3
соответственно равны:
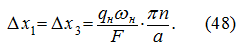
Тогда, если
х
Т
*
– заданное конечное положение поршня, то
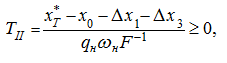
откуда с учетом (48) получим:
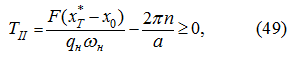
следовательно,
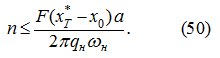
Если обозначить правую часть неравенства (46) через
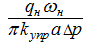 ,
то с учетом (50) должно иметь место неравенство:
,
то с учетом (50) должно иметь место неравенство:
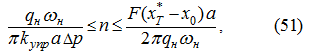
из которого следует, что если оно не выполняется (например, при малых перемещениях
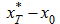 ),
то надо вводить
κq
н
вместо
q
н
, где 0 ≤
κ
≤ 1, то есть уменьшать
q
н
до тех пор, пока не будет выполняться неравенство (51).
),
то надо вводить
κq
н
вместо
q
н
, где 0 ≤
κ
≤ 1, то есть уменьшать
q
н
до тех пор, пока не будет выполняться неравенство (51).
Общее время движения
Т
равно:
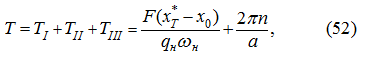
а момент начала торможения:
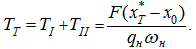 При
t
≥
T
III
получим:
α
= 0,
β
= 0,
v
0
= 0,
w
0
= 0,
то есть система «стоит».
При
t
≥
T
III
получим:
α
= 0,
β
= 0,
v
0
= 0,
w
0
= 0,
то есть система «стоит».
Отметим, что из множества всех допустимых, то есть удовлетворяющих условию (46), значений
n
следует выбрать наименьшее. Это
позволит при прочих равных условиях минимизировать время регулирования
Т
, а также даст возможность обеспечить выполнение
неравенства (51).
На этом этап «грубого» управления окончен.
Описанный алгоритм управления иллюстрируется на рис. 4, где
v
(
t
) и
x
(
t
) – идеализированные
циклограммы скорости и перемещения поршня исполнительного гидроцилиндра.
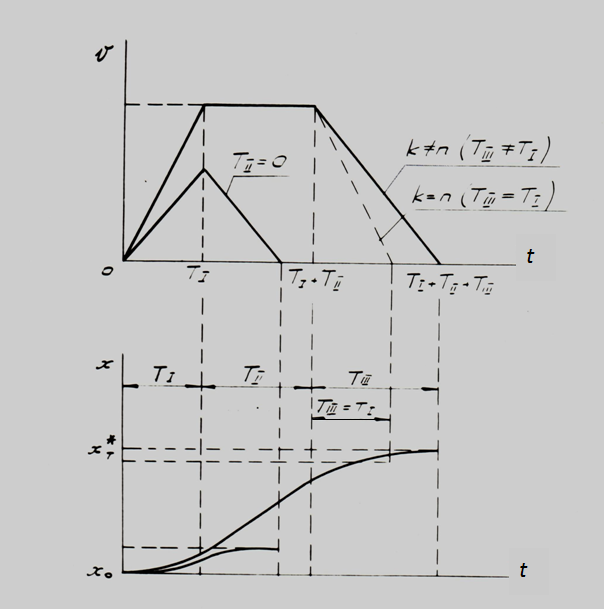
Рис. 4.
|
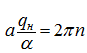 (для того, чтобы в конце разгона
(для того, чтобы в конце разгона