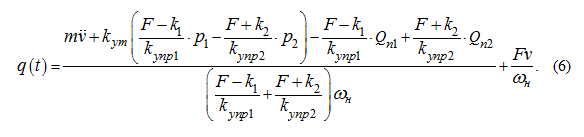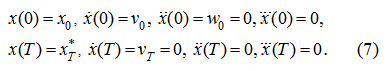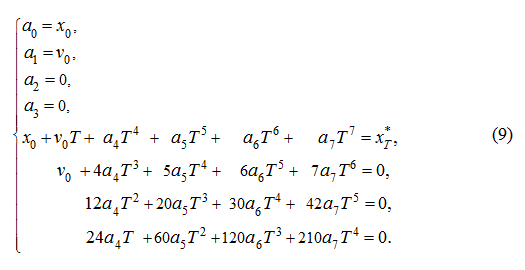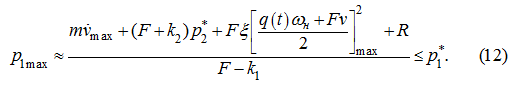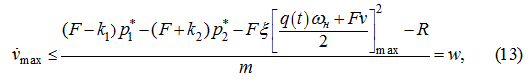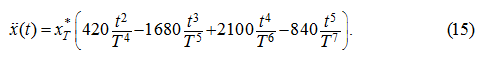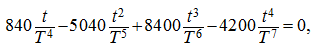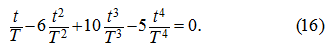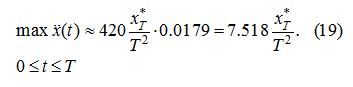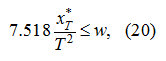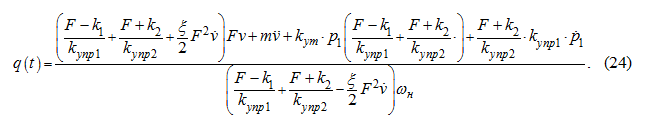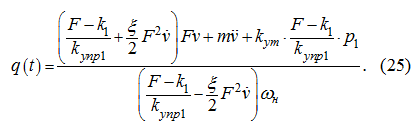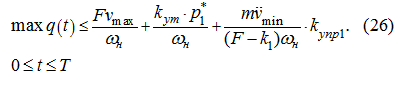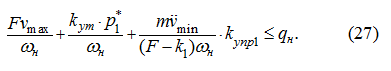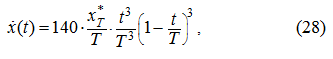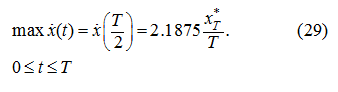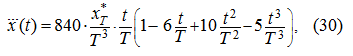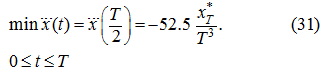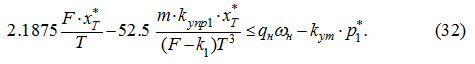|
Системы управления - Динамический синтез - Метод планирования закона движения - Алгоритм
Алгоритм
В отличие от предыдущего этот метод позволяет синтезировать управление без использования частотных характеристик гидропривода.
В наиболее общем случае для планирования закона движения необходимо решать две задачи [1]:
1)
задачу разбиения
всего промежутка времени управления [0,
Т
] на более мелкие отрезки [
t
j
– 1
,
t
j
],
для нахождения граничных точек которых
t
j
(
узлов интерполяции
) часто используют метод последовательных приближений;
2)
задачу интерполяции
– приближения функций (управляющих сигналов)
y
(
t
) на промежутке [0,
Т
]. Один из наиболее
совершенных способов интерполирования функций –
интерполирование
сплайнами
[1, 2].
В рассматриваемой нами постановке задачи об управлении позиционированием груза разбиение промежутка [0,
Т
] на более мелкие отрезки без
ограничения общности не является обязательным. Поэтому в данном случае задача сводится к планированию закона движения груза полиномом
n
-ой
степени, коэффициенты которого определяются, исходя из заданных граничных условий.
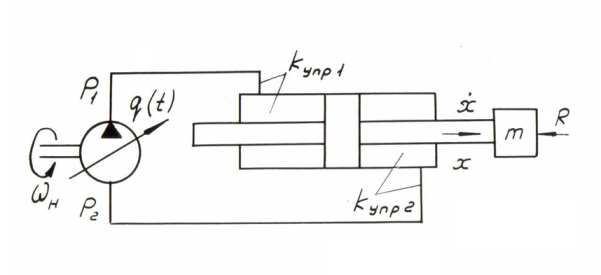
Рис. 1.
Рассмотрим вновь математическую модель гидросистемы (рис. 1), но теперь уже с учетом утечек рабочей жидкости, потерь давления по длине трубопроводов
и в местных сопротивлениях, приняв следующие допущения:
1) потери давления зависят от среднего значения расхода рабочей жидкости на выходе насоса и на входе в гидроцилиндр;
2) приведенные масса и нагрузка на штоке гидроцилиндра, а также частота вращения вала насоса постоянны;
3) параметры рабочей жидкости (плотность, вязкость, модуль объемной упругости) постоянны;
4) динамика механизма управления подачей насоса на данном этапе не рассматривается. Как уже отмечалось, ее учет не представляет принципиальных
трудностей, поскольку эта задача может быть решена после или параллельно рассматриваемой, когда искомая зависимость рабочего объема насоса
q
(
t
) (или хотя бы его текущее численное значение) уже известна. Для этого следует записать математическую модель механизма
управления, выходом которой является
q
(
t
).
Тогда система уравнений динамики гидросистемы (рис. 1) принимает вид:
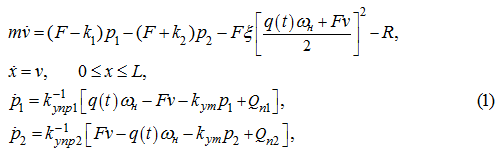
где
Q
n
1
,
Q
n
2
– расходы подпитки в магистралях гидросистемы,
ξ
– приведенный
коэффициент гидравлических сопротивлений; остальные обозначения те же, что и ранее:
m
– приведенная к штоку масса подвижных частей
механизма;
р
1
,
р
2
– давления в напорной и сливной полостях гидросистемы;
x
,
v
–
перемещение и скорость поршня гидроцилиндра;
k
1
,
k
2
– коэффициенты пропорциональности в переменных
составляющих силы трения, зависящих от давления;
R
– постоянная нагрузка на штоке гидроцилиндра;
ω
н
– угловая скорость
вала насоса;
F
– рабочая площадь поршня гидроцилиндра;
q
(
t
) – рабочий объем насоса в функции времени (собственно сигнал
управления);
k
упр
1
,
k
упр
2
– коэффициенты упругости полостей гидросистемы.
Дифференцируя первое из уравнений (1) по
t
, получим:

Подстановка
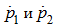 из уравнений (1) в уравнение (2) дает:
из уравнений (1) в уравнение (2) дает:
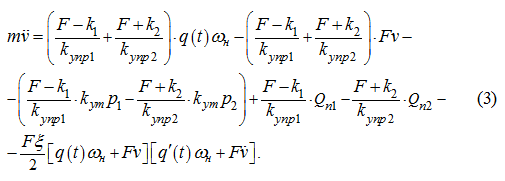
Из уравнения (3) с учетом того, что
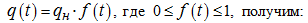
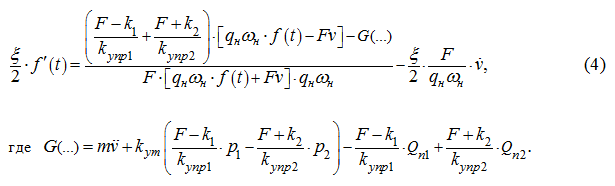
Заметим, что
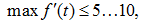 откуда,
пренебрегая левой частью выражения (4), ввиду малости
ξ
(
ξ
≈
1.6·10
-6
)
, окончательно
получим:
откуда,
пренебрегая левой частью выражения (4), ввиду малости
ξ
(
ξ
≈
1.6·10
-6
)
, окончательно
получим:
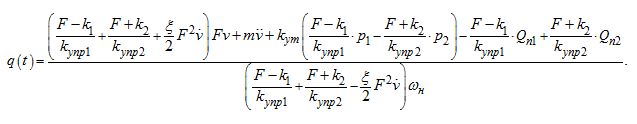 (5)
(5)
Как показали расчеты,
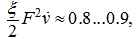 поэтому, если пренебречь этим слагаемым, получим более простую по сравнению с (5) зависимость
q
(
t
):
поэтому, если пренебречь этим слагаемым, получим более простую по сравнению с (5) зависимость
q
(
t
):
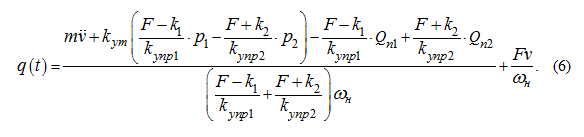
Забегая вперед, отметим, что расчеты переходных процессов в расчетной гидросхеме (рис. 2) при изменении рабочего объема насоса
q
(
t
) по
уравнениям (5) и (6) дали практически одинаковые результаты.
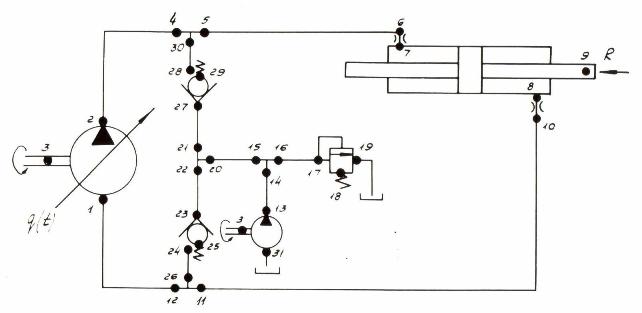
Рис. 2.
Спланировав траекторию
x
(
t
), получим зависимости
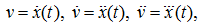 которые затем необходимо подставить в уравнения (5) или (6). Что касается давлений
р
1
и
р
2
, а также
расходов подпитки
Q
n
1
и
Q
n
2
в магистралях гидросистемы, то их определение даже с
помощью упрощенной математической модели (1) через
x
(
t
),
v
(
t
) и их производные является слишком сложным ввиду
имеющихся существенных нелинейностей и высокого порядка системы уравнений, поэтому в процессе синтеза требуемого закона управления
q
(
t
)
подставлялись вместо
р
1
,
р
2
,
Q
n
1
и
Q
n
2
их
численные значения, полученные на каждом шаге времени в результате моделирования, то есть осуществляя аналогию измерения недостающих величин.
Такой метод обеспечивает кроме всего прочего частичную компенсацию возможных погрешностей, появляющихся вследствие упрощенного математического
описания (1) объекта управления. Результат влияния неучтенных факторов в определенной степени отражается на «измеряемых» величинах.
которые затем необходимо подставить в уравнения (5) или (6). Что касается давлений
р
1
и
р
2
, а также
расходов подпитки
Q
n
1
и
Q
n
2
в магистралях гидросистемы, то их определение даже с
помощью упрощенной математической модели (1) через
x
(
t
),
v
(
t
) и их производные является слишком сложным ввиду
имеющихся существенных нелинейностей и высокого порядка системы уравнений, поэтому в процессе синтеза требуемого закона управления
q
(
t
)
подставлялись вместо
р
1
,
р
2
,
Q
n
1
и
Q
n
2
их
численные значения, полученные на каждом шаге времени в результате моделирования, то есть осуществляя аналогию измерения недостающих величин.
Такой метод обеспечивает кроме всего прочего частичную компенсацию возможных погрешностей, появляющихся вследствие упрощенного математического
описания (1) объекта управления. Результат влияния неучтенных факторов в определенной степени отражается на «измеряемых» величинах.
Закон движения
x
(
t
) спланируем, исходя из того, что в период 0 ≤
t
≤
T
необходимо переместить груз из точки
х
0
в точку
x
T
*
при следующих граничных условиях:
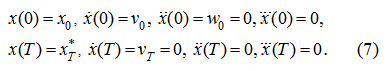
Как видно из зависимости (6) и системы уравнений (1), наличие
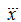 необходимо для определения
q
(
t
). Имея 8 граничных условий (7), спланируем закон движения с помощью полинома 7-ой степени:
необходимо для определения
q
(
t
). Имея 8 граничных условий (7), спланируем закон движения с помощью полинома 7-ой степени:

Из (7) – (8) имеем:
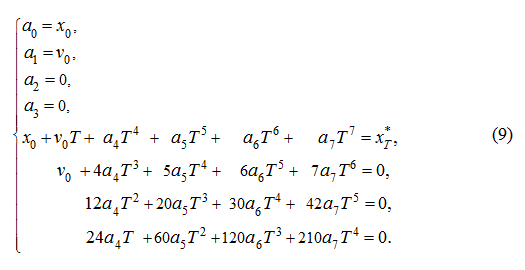
Так как рассматривается перемещение поршня от левого упора (
х
0
= 0,
v
0
= 0), то решая систему уравнений
(9) относительно
а
4
,
а
5
,
а
6
и
а
7
, получим следующие коэффициенты
полинома:
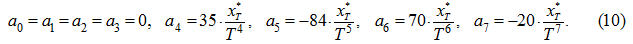
Для определения времени управления
Т
необходимо рассмотреть ряд ограничений, первое из которых накладывается на пиковые давления
р
1max
:
р
1max
≤
р
1
*
, (11)
где
р
1
*
– максимально допустимое давление в напорной полости при разгоне (или в сливной полости при торможении),
соответствующее давлению срабатывания предохранительного клапана. Иными словами, ограничение (11) необходимо для того, чтобы максимальное
быстродействие системы обеспечивалось
без срабатывания предохранительного клапана
, поскольку иначе система становится «плохо управляемой»
(сказывается влияние клапана на переходных процессах), а скорость исполнительных механизмов снижается ввиду перепуска части рабочей жидкости через
клапан.
При условии достаточной подпитки (
р
2
=
р
2
*
) из первого уравнения системы (1) и ограничения (11)
имеем следующую приближенную оценку:
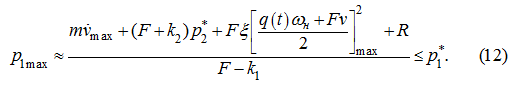
Выражение (12) дает лишь приближенную оценку для
р
1max
, поскольку скорости (расходы) достигают своих максимальных значений
позже, чем ускорение, поэтому фактическое значение пикового давления при заданных параметрах регулирования (
q
(
t
),
Т
и
пр.) будет несколько ниже, а значит, будет обеспечен некоторый запас по давлению
р
1
.
Из (12) получим:
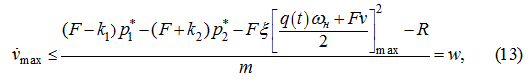
а из (8) и (10) следует:

Дифференцируя (14) дважды по
t
, получим:
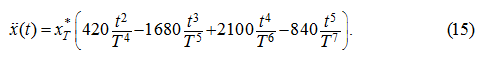
Для нахождения
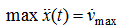 продифференцируем (15) еще раз по
t
и приравняем
продифференцируем (15) еще раз по
t
и приравняем
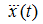 к нулю:
к нулю:
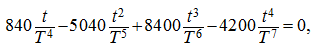
или после упрощений:
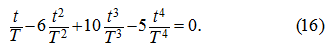
Обозначив
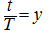 ,
получим следующее уравнение:
,
получим следующее уравнение:
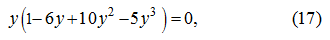
корни которого суть
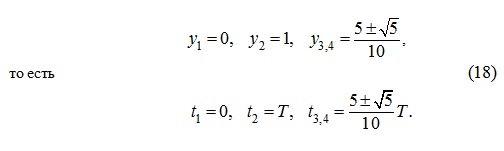
Анализ корней (18) показывает, что
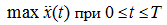 достигается при
достигается при
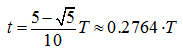 и равен:
и равен:
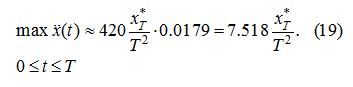
Из (13) и (19) следует:
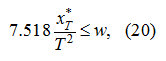
откуда окончательно получим оценку «снизу» для времени
Т
переходного процесса:

Выбрав
Т
из условия (21), необходимо сделать проверку ограничения текущего рабочего объема насоса (сигнала управления):

Непосредственное определение
Т
из условия (22) сопряжено со значительными вычислительными трудностями [см. формулы (5) – (6)], поэтому
ограничимся оценкой
q
(
t
), основанной на следующих допущениях:
1) максимум
q
(
t
) совпадает по времени с
v
max
;
2) изменением давления в сливной магистрали при разгоне можно пренебречь, то есть принять, что
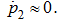
Первое допущение справедливо для достаточно плавных включений гидросистемы, а второе – при обеспечении расхода подпитки, необходимого для
компенсации утечек.
Обратимся вновь к системе (1). Сложив два последних уравнения и учитывая, что
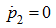 и при разгоне
Q
n
1
= 0, получим:
и при разгоне
Q
n
1
= 0, получим:
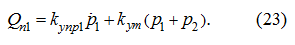
Подстановка (23) в (5) после простых алгебраических преобразований дает:
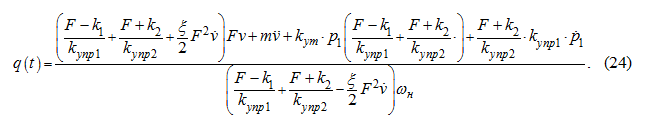
Подстановка в (24) выражения для
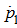 из уравнения (1) после разрешения относительно
q
(
t
) дает:
из уравнения (1) после разрешения относительно
q
(
t
) дает:
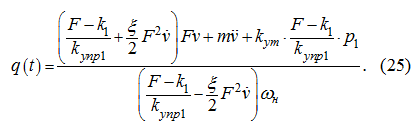
Заметим, что при
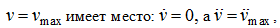 поэтому в соответствии с (25) и первым принятым допущением получим:
поэтому в соответствии с (25) и первым принятым допущением получим:
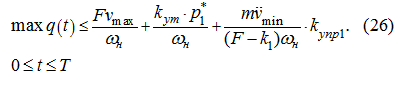
Если правая часть неравенства (26) не превосходит
q
н
, то имеет место неравенство (22), поэтому рассмотрим соотношение:
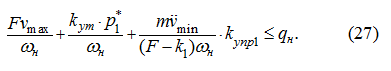
Как следует из (14),
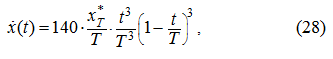
тогда очевидно, что максимум скорости
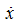 достигается при
достигается при
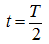 и равен:
и равен:
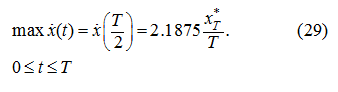
Дифференцируя (28) дважды по
t
, получим выражение:
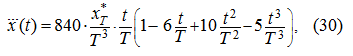
минимум которого достигается при
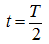 и равен:
и равен:
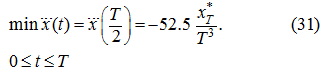
Подставив (29) и (31) в (27) соответственно вместо
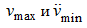 ,
окончательно получим:
,
окончательно получим:
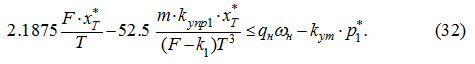
Таким образом, после выбора
Т
из условия (21) необходимо проверить выполнение неравенства (32). Если последнее удовлетворяется при
выбранном значении
Т
, то на этом синтез управления методом планирования закона движения завершается. В противном случае, необходимо
скорректировать
Т
и вновь произвести проверку условия (32). Отметим, что построенный здесь алгоритм определения
Т
в силу
симметрии гидросистемы распространяется и на процесс торможения. Имеющаяся асимметрия усилий (силы трения) пойдет в запас по пиковым давлениям
при торможении, что подтверждается результатами моделирования переходных процессов (см. далее).
|
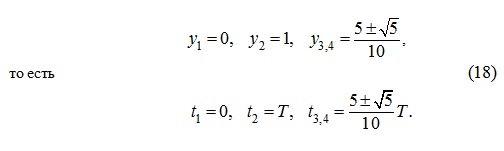
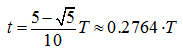 и равен:
и равен:

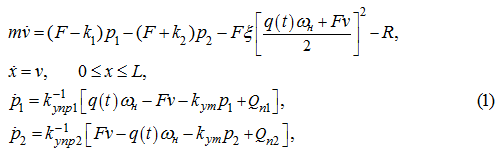
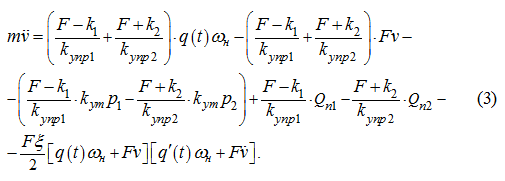
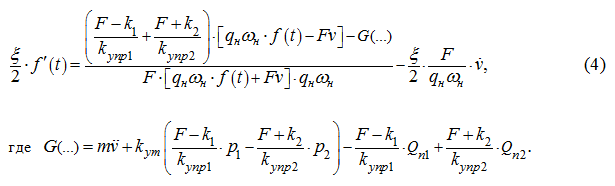
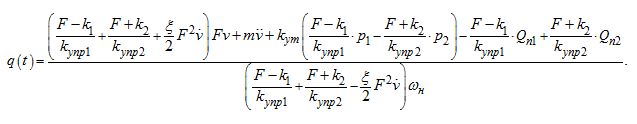 (5)
(5)