|
Структурный анализ транспортной схемы Бетонное хозяйство на строительстве крупных промышленных объектов представляет собой сложную технологическую систему, состоящую из сети конвейерных линий, складов заполнителей бетона, отделений контрольного грохочения, подогрева-охлаждения, обезвоживания, расходных бункеров.Возможны два варианта технологических схем подачи материалов конвейерным транспортом со складов к расходным бункерам бетонных заводов (рис.1).
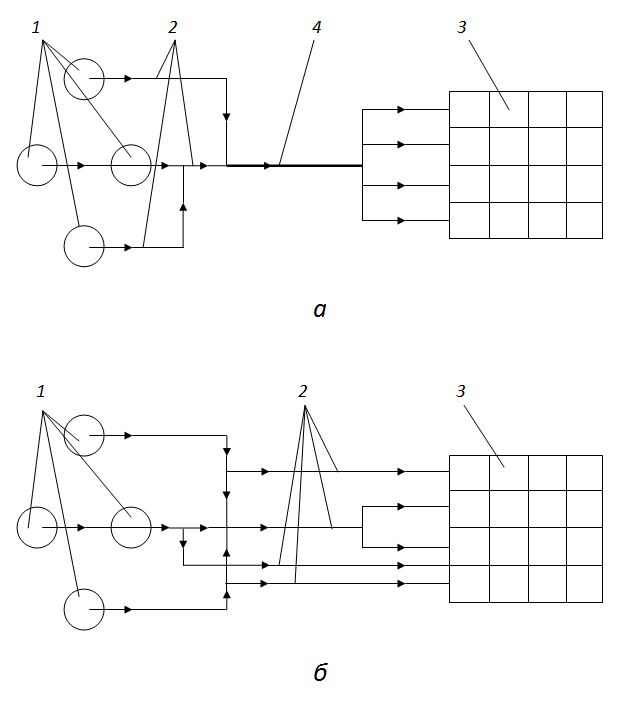
Рис.1. Принципиальные схемы конвейерного транспорта.
В первом случае (рис.1,
а
) материалы, поступающие со склада или с группы складов, подаются к расходным бункерам системой ленточных
конвейеров, причем характерным для этой схемы является наличие магистрального конвейера, объединяющего все потоки материалов. Во втором случае
(рис.1,
б
) материалы, поступающие со складов, не объединяются в один поток, то есть магистральный конвейер отсутствует.
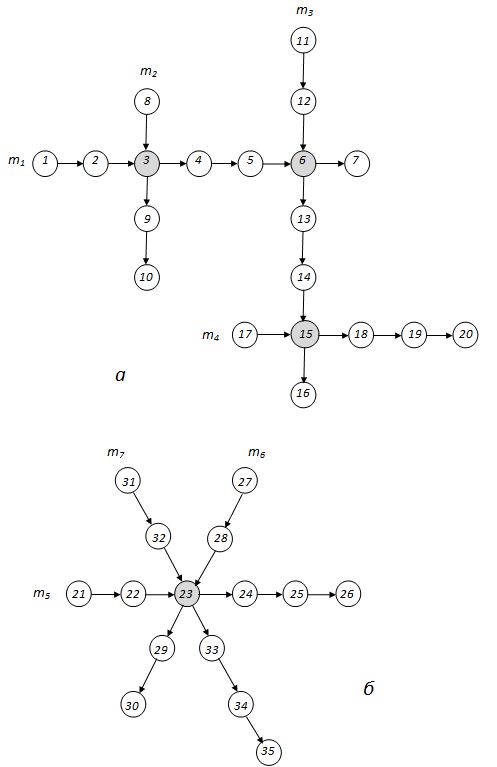
Рис.2. Возможные варианты транспортных маршрутов.
Маршрут
– последовательность конвейеров (рис.2), транспортирующих материалы с одного склада (например,
m
1
= {
1, 2, 3, 4, 5, 6, 7
};
m
2
={
8, 3, 9, 10
}).
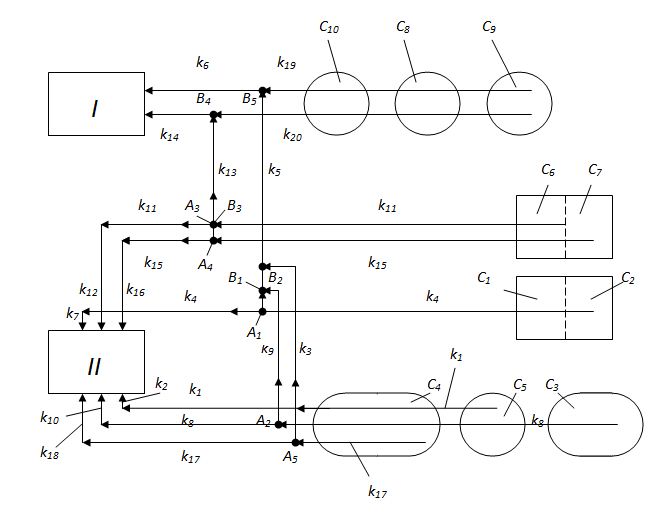
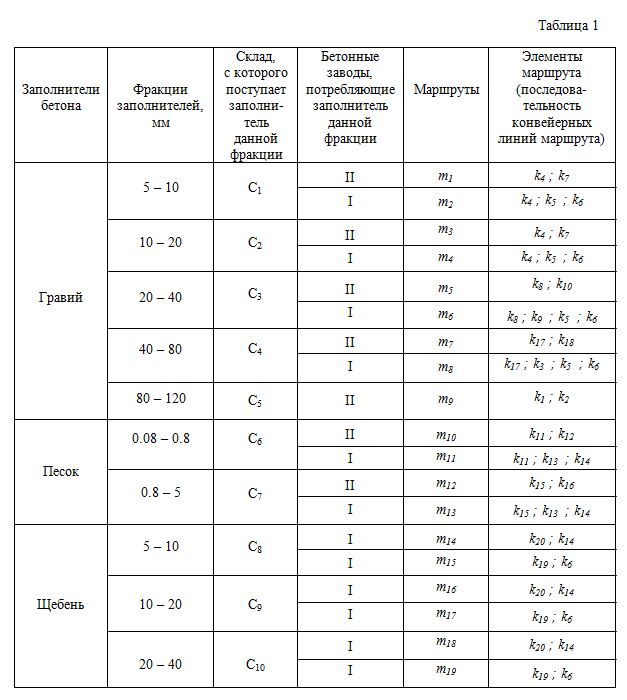
Рис.3. Реальная схема конвейерных линий бетонного хозяйства. По этой схеме заполнители бетона (песок, гравий, щебень) различных фракций подаются со складов C i конвейерными линиями k l к бетонным заводам циклического ( I ) и непрерывного ( II ) действия. В точках A j и B j потоки материалов соответственно разделяются или объединяются. Исходная информация о структуре рассматриваемой транспортной схемы сведена в табл.1.
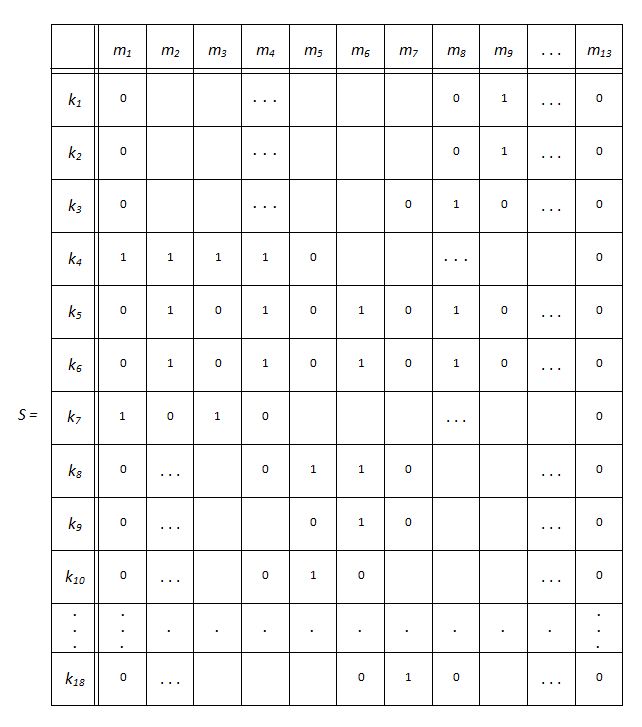
Схема (рис.3) и табл.1 предусматривают возможность использования щебня на заводе циклического действия в качестве заполнителя для некоторых марок бетона. Структурный анализ транспортной схемы проведем для ее первого варианта. Чтобы установить взаимосвязь между отдельными маршрутами, составим на основании табл.1 следующую матрицу S :
Матрица построена следующим образом. Если на пересечении
l
-ой строки и
j
-го столбца матрицы стоит 1, то это означает, что
l
-я конвейерная линия входит в
j
-й маршрут, в противном случае
lj
-й элемент матрицы
S
равен 0.
Рис.4. Технологически независимые участки транспортной схемы. В реальной транспортной схеме это соответствует разбивке всей схемы на три технологически независимых участка (рис.4): транспортирование гравия фракции 80 – 120 мм – узел (рис.4, а ); транспортирование гравия фракций 5 – 10, 10 – 20, 20 – 40 и 40 – 80 мм – сеть (рис.4, б ); транспортирование песка – сеть (рис.4, в ).Управление транспортными потоками заполнителей со складов к расходным бункерам на трех полученных участках может осуществляться независимо. |
Содержание
>> Инженерная математика
>> Системы управления
>> Управление поточно-транспортной системой бетонного хозяйства
>> Структурный анализ транспортной схемы