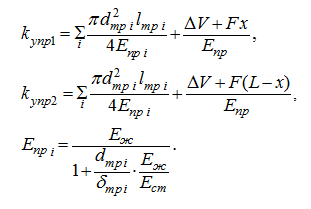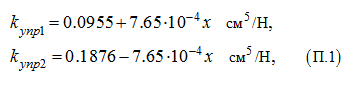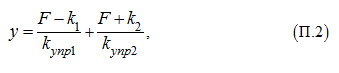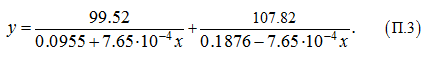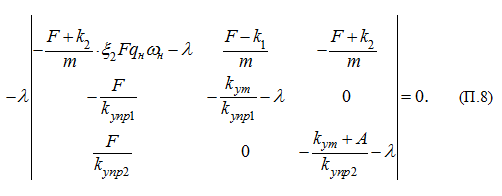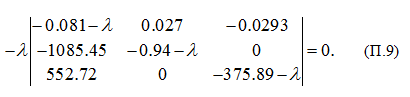Содержание
>> Инженерная математика
>> Системы управления
>> Динамический синтез системы управления объемным гидроприводом
>> Приложение: Оценка влияния переменной упругости, потерь давления и утечек на собственную частоту гидросистемы
|
Системы управления - Динамический синтез - Приложение
Приложение: Оценка влияния переменной упругости, потерь давления по длине
трубопроводов и в местных сопротивлениях и утечек на собственную частоту гидросистемы
Рассмотрим конкретную расчетную схему гидропривода поступательного движения с замкнутой циркуляцией потока
(рис. 5) раздела «Метод кратных периодов собственных колебаний. Пример»
.
На основаниии зависимостей
(6) и (7) из раздела «Метод кратных
периодов собственных колебаний. Алгоритм»
:
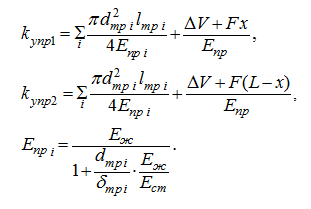
коэффициенты упругости полостей гидросистемы при заданных ее параметрах
(табл. 1 раздела «Метод кратных периодов собственных колебаний. Пример»)
равны:
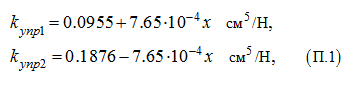
где
х
– перемещение поршня гидроцилиндра в см.
Тогда функция
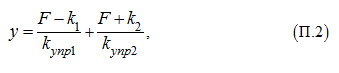
входящая в подкоренное выражение
(1) раздела «Метод кратных периодов
собственных колебаний. Пример»
для определения собственной частоты, при заданных параметрах гидросистемы имеет вид:
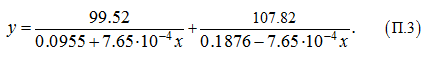
При 0 ≤
х
≤ 120 (полный ход поршня гидроцилиндра)
у
изменяется в пределах: 14.7 ≤
у
≤ 16.65, то есть максимальное
изменение функции
у
при полном ходе поршня гидроцилиндра составит:

В то же время при 0 ≤
х
≤ 64 (заданная точка позиционирования) 14.7 ≤
у
≤ 16.3, то есть
изменение
у
составит ~ 1.107. Таким образом, упругость гидросистемы меняется на ~ 11...13%, следовательно, изменение собственной частоты лежит в
пределах ~ 5...6%. Если же ограничиться рассмотрением диапазона изменения
х
, соответствующего только разгону или торможению, то влияние
переменной упругости на изменение собственной частоты гидросистемы окажется еще меньше и составит ~ 3...4%. Таким образом, имеющееся непостоянство
упругости гидросистемы оказывает весьма незначительное влияние на величину собственной частоты привода.
Рассмотрим уравнения динамики гидросистемы, приведенной на
рис. 5
раздела «Метод кратных периодов собственных колебаний. Пример»
, при разгоне с учетом утечек и потерь давления по длине трубопроводов и в
местных сопротивлениях:

где
ξ
1
,
ξ
2
– приведенные коэффициенты суммарных гидравлических потерь по длине трубопроводов и в местных
сопротивлениях;
р
7
,
р
8
– давления соответственно в напорной и сливной полостях гидроцилиндра;
k
ут
– коэффициент утечек рабочей жидкости;
Q
n
2
– расход подпитки, определяемый по статической
характеристике
(3) раздела «Метод кратных периодов собственных колебаний.
Пример»
.
Функцию
v
2
линеаризуем, разлагая ее в степенной ряд в окрестности
v
0
и удерживая только линейные члены
разложения:
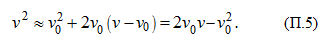
Примем в качестве
v
0
«среднее» значение скорости:

тогда
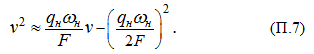
С учетом
(3) из раздела «Метод кратных периодов собственных колебаний.
Пример»
и (П.7) характеристическое уравнение системы (П.4) имеет вид:
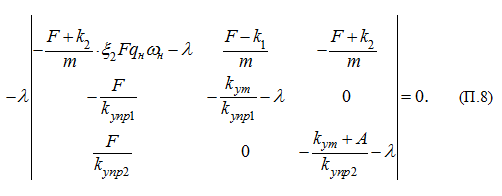
В соответствии с заданными численными значениями параметров
(табл. 1
раздела «Метод кратных периодов собственных колебаний. Пример»)
получим:
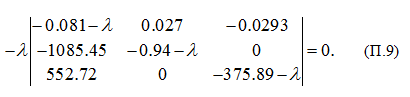
Здесь
А
= 70.4 см
5
/(Н·с),
ξ
1
=
ξ
2
= 8·10
-6
Н·с
2
/см
8
.
Раскрывая определитель в уравнении (П.9), получим следующее характеристическое уравнение:
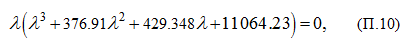
решение которого:
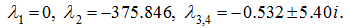
Следовательно, собственная частота гидросистемы равна:
а
= 5.40 рад/с ≈ 0.859 Гц. Из сравнения полученного значения собственной частоты и
ее значения для
3-го расчетного варианта
(~5.42 рад/с) видно, что
учет потерь давления по длине трубопроводов и в местных сопротивлениях, а также учет утечек рабочей жидкости приводит к весьма незначительному
уточнению собственной частоты (~0.4%), но к более ощутимой поправке в коэффициенте демпфирования (без учета указанных факторов этот коэффициент
примерно равен 0.0215, а с их учетом ~0.532). При этом логарифмический декремент затухания составляет ~0.62.
|