Алгоритмы формирования и решения математической модели схемыФормирование исходных данных. Вся исходная информация для проведения динамического анализа схем механического и гидромеханического привода состоит из двух частей: - информация о структуре рассматриваемой схемы привода;
- информация о физических и конструктивных параметрах элементов гидросхемы.
Первая часть исходной информации строится в соответствии с изложенным выше методом структурного описания произвольных гидромеханических схем приводов, основанном на классификации базовых элементов привода , введении понятия обобщенного трехузлового элемента с узлами i (вход), j (выход) и k (управление, преобразование энергии, подвод или отбор мощности). На основании введенной классификации (табл. 1) каждый элемент привода получил определенный идентификатор е , обозначающий тип элемента и однозначно определяющий группу уравнений для математического описания элемента данного типа. В соответствии с этим разработаны специальные формы (таблицы) исходных данных. Каждый типовой элемент привода описывается строкой таблицы исходных данных, имеющей следующую структуру:
где
n
– номер элемента;
А
– матрица-строка коэффициентов, характеризующих физические, геометрические и конструктивные параметры элемента, что составляет содержание второй части исходной информации.
У элементов, имеющих только два узла (например, дизель, фрикционная и гидродинамическая муфты, упругий вал, маховик) третий узел обозначен нулем. Номер элемента
n
предназначен для выбора нужного массива коэффициентов из общего поля исходных данных при формировании системы уравнений.
Формирование математической модели схемы привода в целом. В результате анализа строки таблицы исходных данных каждого элемента и структурного анализа схемы с разбиением ее на участки строится система дифференциальных уравнений динамики гидромеханического привода, имеющая в общем случае следующую структуру:
Алгоритм формирования системы уравнений (63) сводится к следующему.
На первом этапе
формируются уравнения участков (63
а
и
в
). Для этого заранее подсчитываются значения приведенных моментов инерции
На втором этапе формируются уравнения (63 б ), число которых равно числу упругих валов в схеме привода, и уравнения (63 г ) перемещений машины и муфты регулятора дизеля. Внешние возмущения и сигналы управления. Информация о внешних возмущениях и сигналах управления задается специальной таблицей исходных данных (рис. 8).
Рис. 8. Задание внешних возмущений и сигналов управления
Алгоритм решения. Для интегрирования систем дифференциальных уравнений в настоящее время существует огромное множество методов численного интегрирования (методы Рунге-Кутта, Эйлера и их модификации, метод Гира и т.д.), на базе которых разработана масса различных модификаций соответствующих программ, что позволяет всегда выбрать подходящий аппарат решения. |
Содержание
>> Инженерная математика
>> Гидромеханические приводы и трансмиссии
>> Динамический анализ
>> Алгоритмы формирования и решения математической модели схемы
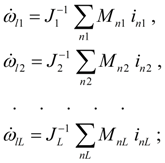 (63
а
)
(63
а
)
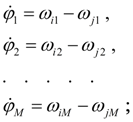 (63
б
)
(63
б
)
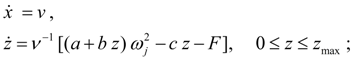 (63
г
)
(63
г
)
