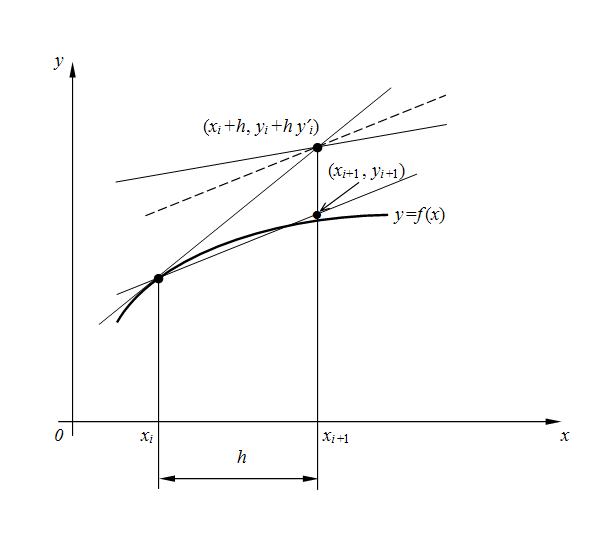Дифференциальные уравнения - Метод Эйлера
Метод Эйлера
Рассмотрим дифференциальное уравнение
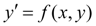 (1)
(1)
с начальным условием
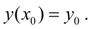
Подставив
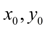 в уравнение (1), получим значение производной в точке
в уравнение (1), получим значение производной в точке
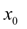 :
:
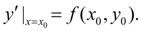
При малом
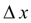 имеет место:
имеет место:
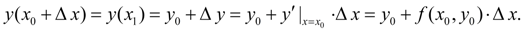
Обозначив
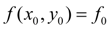 , перепишем последнее равенство в виде:
, перепишем последнее равенство в виде:
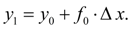 (2)
(2)
Принимая теперь
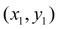 за новую исходную точку, точно также получим:
за новую исходную точку, точно также получим:
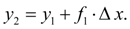
В общем случае будем иметь:
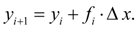 (3)
(3)
Это и есть
метод Эйлера
. Величина
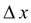 называется
шагом интегрирования
. Пользуясь этим методом, мы получаем приближенные значения
у
, так как производная
называется
шагом интегрирования
. Пользуясь этим методом, мы получаем приближенные значения
у
, так как производная
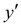 на самом деле не остается постоянной на промежутке длиной
на самом деле не остается постоянной на промежутке длиной
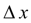 . Поэтому мы получаем ошибку в определении значения функции
у
, тем большую, чем больше
. Поэтому мы получаем ошибку в определении значения функции
у
, тем большую, чем больше
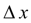 . Метод Эйлера является простейшим методом численного интегрирования дифференциальных уравнений и систем. Его недостатки – малая точность и систематическое накопление ошибок.
. Метод Эйлера является простейшим методом численного интегрирования дифференциальных уравнений и систем. Его недостатки – малая точность и систематическое накопление ошибок.
Более точным является
модифицированный метод Эйлера с пересчетом
. Его суть в том, что сначала по формуле (3) находят так называемое «грубое приближение» (прогноз):
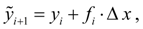
а затем пересчетом
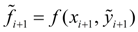 получают тоже приближенное, но более точное значение (коррекция):
получают тоже приближенное, но более точное значение (коррекция):
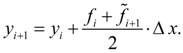 (4)
(4)
Фактически пересчет позволяет учесть, хоть и приблизительно, изменение производной
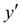 на шаге интегрирования
на шаге интегрирования
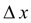 , так как учитываются ее значения
, так как учитываются ее значения
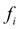 в начале и
в начале и
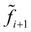 в конце шага (рис. 1), а затем берется их среднее. Метод Эйлера с пересчетом (4) является по существу методом Рунге-Кутта 2-го порядка [2], что станет очевидным из дальнейшего.
в конце шага (рис. 1), а затем берется их среднее. Метод Эйлера с пересчетом (4) является по существу методом Рунге-Кутта 2-го порядка [2], что станет очевидным из дальнейшего.
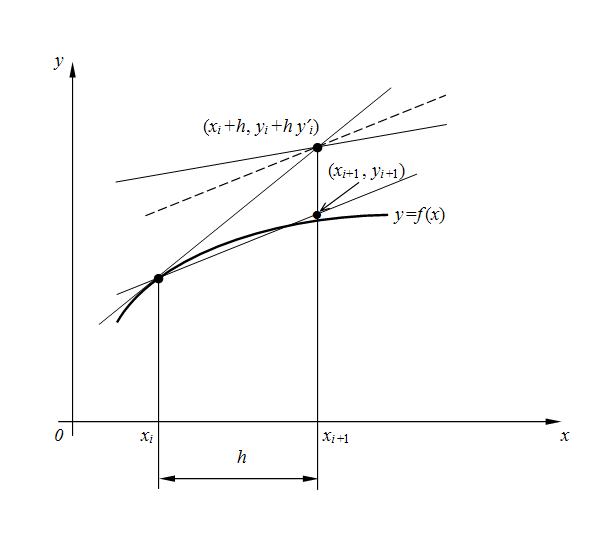
Рис. 1. Геометрическое представление метода Эйлера с пересчетом.
|
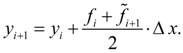 (4)
(4)