Интерполирование сплайнами
Интерполяционные формулы Лагранжа, Ньютона и Стирлинга и др. при использовании большого числа узлов интерполяции на всем отрезке [
a
,
b
] часто приводят к плохому приближению из-за накопления погрешностей в процессе вычислений [2]. Кроме того, из-за расходимости процесса интерполяции увеличение числа узлов не обязательно приводит к повышению точности. Для снижения погрешностей весь отрезок [
a
,
b
] разбивается на частичные отрезки и на каждом из них функцию
Один из способов интерполирования на всем отрезке [
a
,
b
] является
интерполирование сплайнами
.
Сплайном
называется кусочно-полиномиальная функция, определенная наотрезке [
a
,
b
] и имеющая на этом отрезке некоторое количество непрерывных производных. Преимущества интерполяции сплайнами по сравнению с обычными методами интерполяции – в сходимости и устойчивости вычислительного процесса.
Рассмотрим один из наиболее распространенных в практике случаев – интерполирование функции
кубическим сплайном
.
и обозначим
Сплайном, соответствующим данной функции
1) на каждом отрезке
2) функция
3)
Третье условие называется
условием интерполирования
. Сплайн, определяемый условиями 1) – 3), называется
интерполяционным кубическим сплайном
.
Рассмотрим способ построения кубического сплайна [2].
На каждом из отрезков
где
Продифференцируем (7) трижды по х :
откуда следует
Кроме того, будем считать
Из условий непрерывности функции
Обозначив
В силу трехдиагональности матрицы коэффициентов система (9) имеет единственное решение [2]. Найдя коэффициенты
Таким образом, существует и найден единственный кубический сплайн, удовлетворяющий условиям 1) – 3) . |
Содержание
>> Прикладная математика
>> Численные методы
>> Интерполяция функций
>> Интерполирование сплайнами
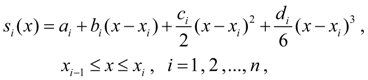 (7)
(7)
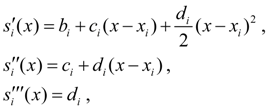
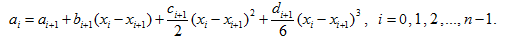
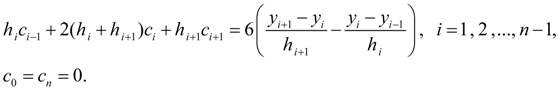 (9)
(9)
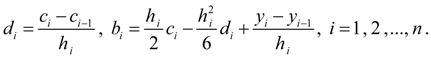 (10)
(10)