Примеры [2]

П р и м е р 1. Поезда метрополитена идут регулярно с интервалом 2 мин. Пассажир выходит на перрон в случайный момент времени, никак не связанный с расписанием. Случайная величина – время Т , в течение которого ему придется ждать поезда. Найти плотность распределения, математическое ожидание, дисперсию, среднее квадратичное отклонение и вероятность того, что ждать пассажиру придется не больше полминуты.

Р е ш е н и е . Плотность распределения f ( x ) =1/2  (0 < x < 2) показана на рис. 9.

Рис. 9. Плотность распределения

П р и м е р 2. Случайная величина Х имеет показательное распределение с параметром . Найти вероятность события {1 < X < 2}.

Р е ш е н и е . Имеем Вероятность попадания в интервал (1, 2) равна приращению функции распределения на этом интервале:

П р и м е р 3. Матрица распределения системы двух случайных величин X и Y задана таблицей:

Найти числовые характеристики системы случайных величин ( X , Y ): математические ожидания , дисперсии , средние квадратичные отклонения , ковариацию и коэффициент корреляции .

Р е ш е н и е . Сначала найдем ряды распределения отдельных величин, входящих в систему. Суммируя вероятности p i j , стоящие в 1-ой, 2-ой и 3-ей строках, получим:

Ряд распределения случайной величины X имеет вид:

Математическое ожидание
По формуле (8) дисперсия
Среднее квадратичное отклонение

Аналогично суммируя вероятности p i j , стоящие в 1-ом, 2-ом и 3-ем столбцах, получим:

Ряд распределения случайной величины Y имеет вид:

Математическое ожидание
По формуле (8) дисперсия
Среднее квадратичное отклонение

Ковариация по формуле (52)
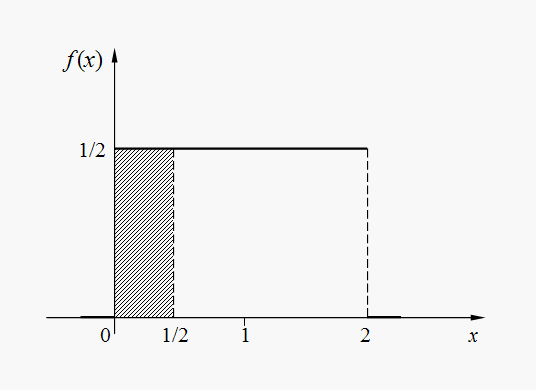
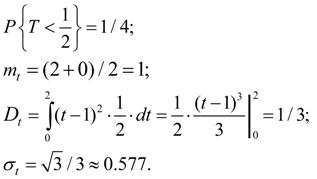
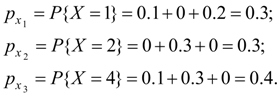
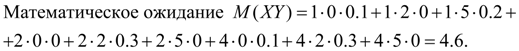
Коэффициент корреляции: таким образом между случайными величинами X и Y имеется отрицательная линейная корреляция, т.е. при увеличении одной из них другая имеет уменьшается.