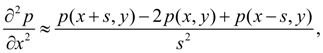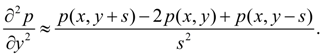Метод конечных разностей (метод сеток)
Идея
метода конечных разностей (метода сеток)
известна давно, с соответствующих трудов Эйлера. Однако практическое применение этого метода было тогда весьма ограничено из-за огромного объема ручных вычислений, связанных с размерностью получаемых систем алгебраических уравнений, на решение которых требовались годы. В настоящее время, с появлением быстродействующих компьютеров, ситуация в корне изменилась. Этот метод стал удобен для практического использования и является одним из наиболее эффективных при решении различных задач математической физики.
Основная идея
метода конечных разностей (метода сеток)
для приближенного численного решения краевой задачи для двумерного дифференциального уравнения в частных производных состоит в том, что
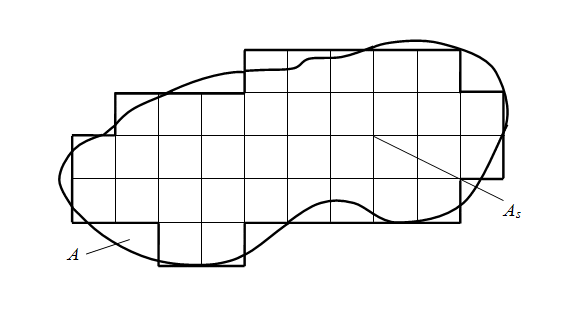
1) на плоскости в области
А
, в которой ищется решение, строится
сеточная область
А
s
(рис.1), состоящая из одинаковых ячеек размером
s
(
s
– шаг сетки) и являющаяся приближением данной области
А
;
2) заданное дифференциальное уравнение в частных производных заменяется в узлах сетки А s соответствующим конечно-разностным уравнением; 3) с учетом граничных условий устанавливаются значения искомого решения в граничных узлах области А s .
Решая полученную систему конечно-разностных алгебраических уравнений, получим значения искомой функции в узлах сетки А s , т.е. приближенное численное решение краевой задачи. Выбор сеточной области А s зависит от конкретной задачи, но всегда надо стремиться к тому, чтобы контур сеточной области А s наилучшим образом аппроксимировал контур области А . Рассмотрим уравнение Лапласа
где p ( x , y ) – искомая функция, x , y – прямоугольные координаты плоской области и получим соответствующее ему конечно-разностное уравнение.
Заменим частные производные
Тогда решая уравнение (1) относительно p ( x , y ), получим:
Задав значения функции
p
(
x
,
y
) в граничных узлах контура сеточной области
А
s
в соответствии
с граничными условиями и решая полученную систему уравнений (2) для каждого узла сетки, получим численное решение краевой задачи (1) в заданной области
А
.
Ясно, что число уравнений вида (2) равно количеству узлов сеточной области А s , и чем больше узлов (т.е. чем мельче сетка), тем меньше погрешность вычислений. Однако надо помнить, что с уменьшением шага s возрастает размерность системы уравнений и следовательно, время решения. Поэтому сначала рекомендуется выполнить пробные вычисления с достаточно крупным шагом s , оценить полученную погрешность вычислений, и лишь затем перейти к более мелкой сетке во всей области или в какой-то ее части. |
Содержание
>> Прикладная математика
>> Численные методы
>> Уравнения математической физики
>> Метод конечных разностей / Метод сеток
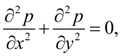 (1)
(1)