Примеры

П р и м е р 1. Решить кубическое уравнение 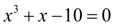с относительной точностью 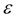=0.001 методом касательных Ньютона-Рафсона.
Р е ш е н и е . В данном случае 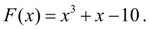Следовательно, В качестве нулевого приближения примем 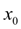=3 (точное значение корня 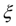=2). Тогда по формуле (7) получим:

,
,

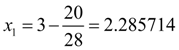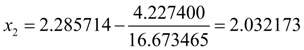Проверим, достигнута ли заданная относительная точность :

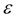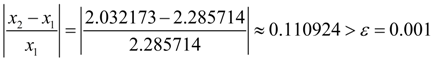
Продолжим итерации:

.

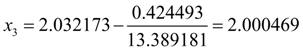Вновь проверим, достигнута ли заданная относительная точность :

.

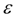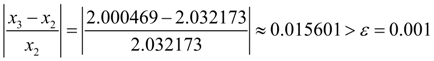Следующая итерация с точностью до 6-ти десятичных знаков дает практически точное значение корня:

.

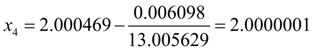Однако, и здесь следует проверить, достигнута ли заданная относительная точность :

.

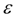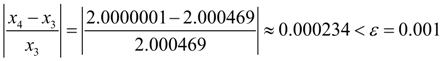Найденный корень уравнения равен 2.0000001. Таким образом, вычислительный процесс сошелся за 4 итерации, и мы получили искомый корень с заданной относительной точностью .

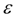П р и м е р 2. Решить кубическое уравнение 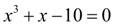с относительной точностью 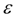=0.001 методом итераций.
Р е ш е н и е . Перепишем заданное уравнение в виде (3):

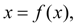
где

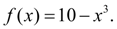
Тогда по формуле (4) получим:

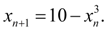
Условие сходимости в данном случае имеет вид: 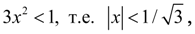но в этом интервале нет корней уравнения 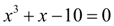. Более того, для функции 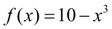в окрестности корня 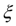=2 имеет место неравенство 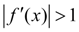, т.е. условие сходимости не выполняется и искать решение уравнения в виде 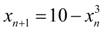не имеет смысла, так как численный процесс будет расходящимся. Поэтому следует записать данное уравнение по-другому:

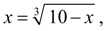
тогда 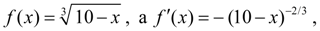и очевидно, что в окрестности корня 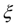=2 здесь имеет место неравенство: 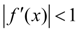, следовательно, выполняется условие сходимости. Поэтому решение данного кубического уравнения будем искать по формуле:

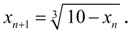
Примем вновь в качестве нулевого приближения 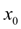=3. Тогда получим:

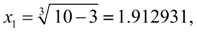
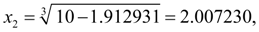
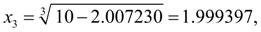
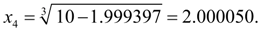
На этом шаге заданная относительная точность 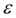достигнута:

,

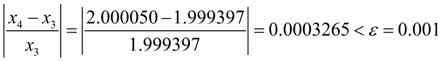поэтому процесс нахождения корня уравнения может считаться завершенным. Найденный корень уравнения равен 2.000050. Таким образом, и здесь искомый корень найден за 4 итерации с заданной относительной точностью .

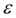П р и м е р 3. Решить кубическое уравнение 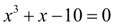с относительной точностью 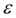=0.001 методом хорд.
Р е ш е н и е . Здесь 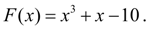Будем искать решение на отрезке [0, 4] (напомним, что точное значение корня 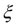=2). В качестве нулевого приближения примем 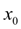=0. Тогда по формуле (12) получим:






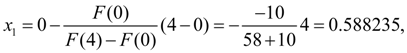
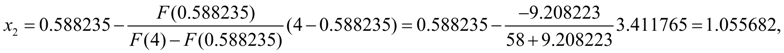
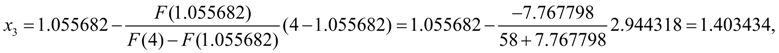
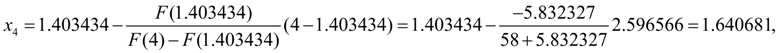
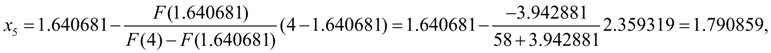
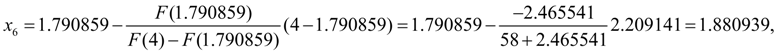
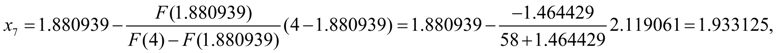
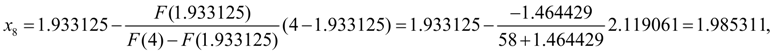
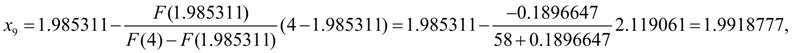
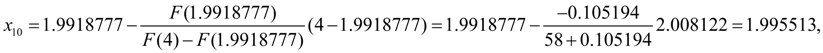
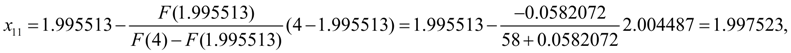
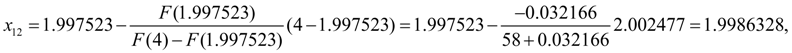
На этом шаге заданная относительная точность 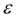достигнута:

,

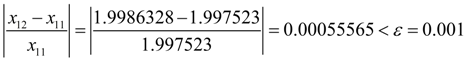и таким образом, процесс нахождения корня может считаться завершенным. Найденный корень уравнения равен 1.9986328. Здесь искомый корень уравнения с заданной относительной точностью 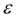получен за 12 итераций.

П р и м е р 4. Решить кубическое уравнение методом половинного деления с точностью 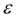=0.001.
Р е ш е н и е . Здесь 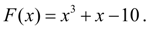В качестве начального рассмотрим отрезок [0, 3], так как его концах функция F ( x ) принимает разные знаки: 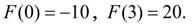Тогда согласно условию сходимости (11) в данном примере получим:

,

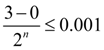откуда следует 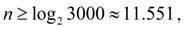т.е. для достижения заданной точности решения этого уравнения методом половинного деления на отрезке [0, 3] потребуется не менее 12 итераций.
Последовательность действий методом половинного деления сводится к следующему: на каждом шаге рассматриваем очередной отрезок, делим его пополам и вычисляем значение функции F ( x ) в середине этого отрезка, выбираем ту половину отрезка, на концах которой F ( x ) имеет  разные знаки. Результаты проведенных последовательных действий по методу половинного деления сведены в таблицу:

На 12-ом шаге в соответствии с оценкой (11) достигается заданная точность решения: 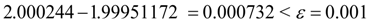, следовательно, для решения этого уравнения с заданной точностью методом половинного деления на отрезке [0, 3] потребовалось, как и ожидалось, 12 итераций. Найденный корень уравнения равен 1.999878. Заметим, что, если бы в данном примере мы рассмотрели отрезoк [0, 4] в качестве начального, то уже на первой итерации получили бы точное решение уравнения, так как
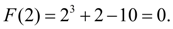
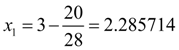
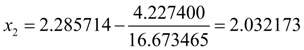
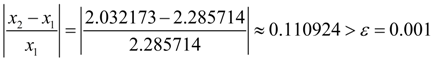
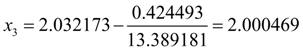
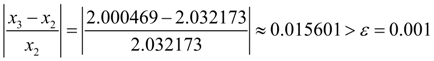
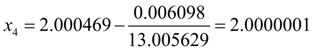
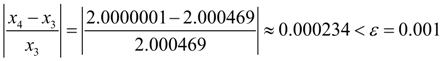
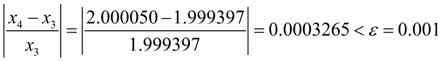
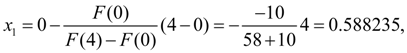
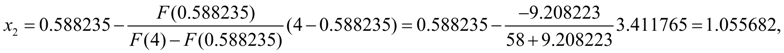
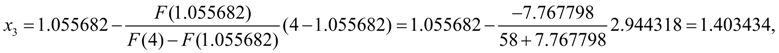
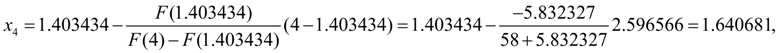
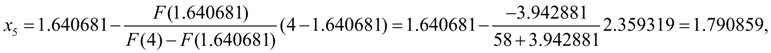
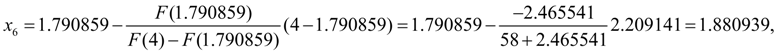
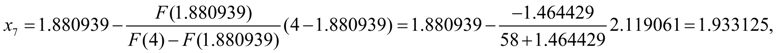
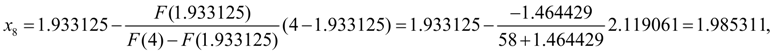
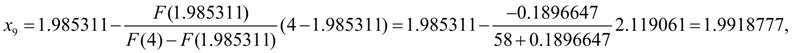
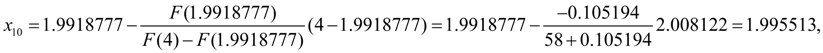
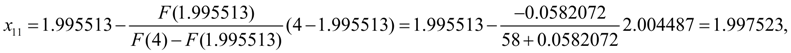
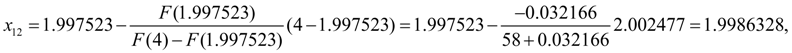
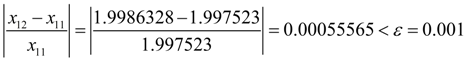
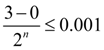