Метод хорд (метод пропорциональных частей)Вновь обратимся к уравнению (1):
где функция
F
(
x
) – непрерывна и определена на некотором отрезке
Затем рассматриваем отрезки
|
Содержание
>> Прикладная математика
>> Численные методы
>> Алгебраические и трансцендентные yравнения
>> Метод хорд
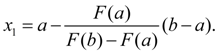 (12)
(12)
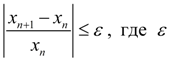 – заданная точность решения. Геометрически этот метод равносилен замене кривой
у =
F
(
x
) хордой, проведенной сначала через точки
– заданная точность решения. Геометрически этот метод равносилен замене кривой
у =
F
(
x
) хордой, проведенной сначала через точки
