|
Метод решения Для решения системы нелинейных уравнений (1) применим итерационный метод Ньютона-Рафсона , общая схема которого сводится к следующему. Пусть задана система нелинейных уравнений вида:
где
Система линеаризованных уравнений (3) в матричной форме может быть приведена к виду:
где
A
[
где
Таким образом, на
n
–ой итерации по значениям
Сходимость итерационного процесса Ньютона-Рафсона в значительной мере зависит от выбора нулевого приближения.
Таким образом, алгоритм Ньютона-Рафсона сводится к последовательному выполнению следующих этапов решения задачи:
1) линеаризация (3) исходных уравнений в окрестности предыдущей итерации (нулевого приближения);
2) задание исходных данных и нулевого приближения;
3) формирование на каждой итерации матрицы Якоби и столбца правых частей для системы линеаризованных уравнений (5);
4) решение на каждой итерации сформированной системы линейных уравнений (5), например методом Гаусса;
5) сравнение двух соседних итераций по условию сходимости (6) с заданной точностью.
Линеаризация уравнений
является необходимым подготовительным этапом, в результате которого строится алгоритм и программа решения задачи тягового расчета. Для реализации итерационного процесса все графические характеристики
Исходные данные
и
нулевое приближение
задаются пользователем-расчетчиком непосредственно перед запуском программы расчета. Остальные пункты 3) – 5) реализуются автоматически в ходе выполнения программы.
Если условие (6) выполнено, то итерационный цикл для данного значения
Т
заканчивается, вычисляются мощность и КПД двигателя, гидротрансформатора, тяговая мощность, часовой расход топлива и ряд других показателей, значение
Т
увеличивается на величину заданного шага Δ
Т
и определяются неизвестные по новому итерационному циклу. В результате получается тяговая характеристика, соответствующая всему диапазону изменения тягового усилия
Т
. Если условие (6) не выполняется, то итерационный цикл для данного значения
Т
либо продолжается до его выполнения, либо прерывается при слишком большом числе проведенных итераций (свыше 20-ти). В этом случае выдается соответствующее сообщение и пользователю необходимо проверить и возможно скорректировать некоторые параметры расчета (изменить нулевое приближение, шаг Δ
Т
, увеличить допуск
|
Содержание
>> Инженерная математика
>> Мобильные машины
>> Тяговый расчет
>> Одномоторная трансмиссия
>> Метод решения
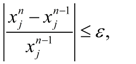 j
= 1, … ,
N
. (6)
j
= 1, … ,
N
. (6)
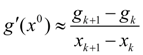 , причем
, причем