Приводы и трансмиссии - Блокировка муфт
Блокировка фрикционных муфт и гидротрансформаторов
Выше (см.
«Введение»
) отмечалось, что особенностью переходных процессов в механических и гидромеханических приводах является наличие в блокируемых элементах (фрикционных муфтах и блокируемых гидротрансформаторах) двух основных режимов:
-
вращение ведущей и ведомой частей с проскальзыванием (пробуксовкой);
-
вращение ведущей и ведомой частей без проскальзывания (режим блокировки).
Известное решение задачи моделирования режима блокировки в механической передаче с одним блокируемым элементом [1, 5, 7], для фрикциона, например, сводится [5] к классической задаче о модели сухого трения при нулевой скорости движущейся массы [6]. Что касается моделирования приводов со многими блокируемыми элементами (как это имеет место, например, в современных гидромеханических трансмиссиях мобильных машин), то эта задача сопряжена с определенными трудностями, так как условия блокировки каждого блокируемого элемента зависят от структуры схемы, распределения внешних моментов и приведенных моментов инерции, а также режима вращения других блокируемых элементов, входящих в рассматриваемую схему привода.
При моделировании режима блокировки вращающихся масс фрикционных муфт и блокируемых гидротрансформаторов можно осуществить стыковку участков, граничащих с этими элементами, объединив их в один участок, и сделать пересчет приведенных моментов инерции, перейдя таким образом к системе уравнений более низкого порядка [1].
Так,
при разблокированных массах
система уравнений, описывающих динамику муфты, имеет вид:
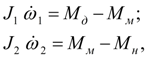 (36)
(36)
где
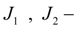 приведенные моменты инерции 1-го и 2-го участков, примыкающих, соответственно к ведущей и ведомой частям муфты;
приведенные моменты инерции 1-го и 2-го участков, примыкающих, соответственно к ведущей и ведомой частям муфты;
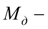 движущий момент;
движущий момент;
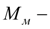 момент, передаваемый муфтой;
момент, передаваемый муфтой;
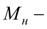 нагрузочный момент;
нагрузочный момент;
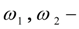 угловые скорости ведущей и ведомой полумуфт.
угловые скорости ведущей и ведомой полумуфт.
При блокировке
уравнения (36) трансформируются к виду:
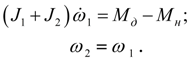 (37)
(37)
Однако, при частой смене режима блокировки и разблокированного состояния муфты при таком подходе возникает ряд трудностей, связанных с возможным и частым изменением структуры схемы и системы дифференциальных уравнений. Иными словами, потребуется постоянный контроль режимов работы этих элементов, пересчет моментов инерции и принятие определенных мер по изменению расчетной схемы. Это приведет к усложнению алгоритма решения и гораздо бо’льшим затратам времени вычислений.
Ниже изложен метод формирования уравнений, позволяющий при моделировании динамики участков схемы независимо от состояния блокируемых масс сохранять структуру системы уравнений неизменной. Покажем, что переход от уравнений вида (36) к уравнениям вида (37) не является обязательным, поскольку при корректном определении момента
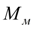 оба режима вращения муфты можно моделировать, пользуясь системой уравнений вида (36), не нарушая тем самым структуру сформированной общей системы уравнений.
оба режима вращения муфты можно моделировать, пользуясь системой уравнений вида (36), не нарушая тем самым структуру сформированной общей системы уравнений.
Условия блокировки фрикционов и гидротрансформаторов.
Пусть
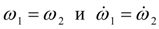 , т.е. произошла блокировка полумуфт. Тогда из уравнений (36) следует:
, т.е. произошла блокировка полумуфт. Тогда из уравнений (36) следует:
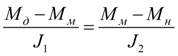 , (38)
, (38)
откуда
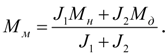 (39)
(39)
Подставляя выражение (39) для
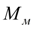 в уравнения (36), получим:
в уравнения (36), получим:
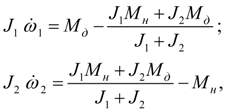 (40)
(40)
откуда следует:
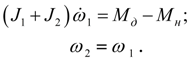 (41)
(41)
Таким образом, если
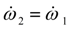 , то имеет место (39), и наоборот. Следовательно,
условием применения уравнений
(
36
)
в режиме блокировки является выполнение равенства
(
39
)
и равенства угловых скоростей ведущей и ведомой полумуфт
, то имеет место (39), и наоборот. Следовательно,
условием применения уравнений
(
36
)
в режиме блокировки является выполнение равенства
(
39
)
и равенства угловых скоростей ведущей и ведомой полумуфт
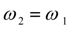 .
.
Рассмотрим равенство
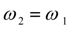 и выясним, какому условию на моменты
и выясним, какому условию на моменты
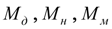 оно эквивалентно.
оно эквивалентно.
Проинтегрируем уравнения (36) один раз по
t
и разрешим их относительно
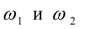 :
:
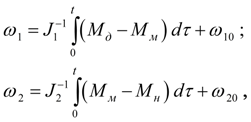 (42)
(42)
где
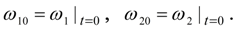
Из условия равенства скоростей
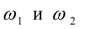 следует:
следует:
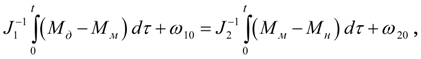 (43)
(43)
откуда
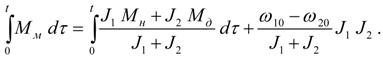 (44)
(44)
С другой стороны, если имеет место (44), то его подстановка в систему (42) дает
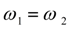 .
.
Таким образом, условия
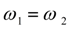 и (44) эквивалентны.
и (44) эквивалентны.
Анализ условий блокировки муфт.
Введем обозначения:
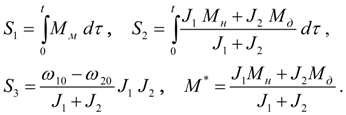 (45)
(45)
Пусть предельный момент, развиваемый муфтой
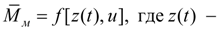 сигнал управления,
u
–
внешняя характеристика (для фрикционной муфты, например, сигналом управления является давление в механизме прижатия дисков фрикционной пары
p
(
t
) , а внешней характеристикой – зависимость коэффициента трения от разности угловых скоростей вращения дисков).
сигнал управления,
u
–
внешняя характеристика (для фрикционной муфты, например, сигналом управления является давление в механизме прижатия дисков фрикционной пары
p
(
t
) , а внешней характеристикой – зависимость коэффициента трения от разности угловых скоростей вращения дисков).
На рис. 6 представлены зависимости моментов и угловых скоростей от времени
t
.
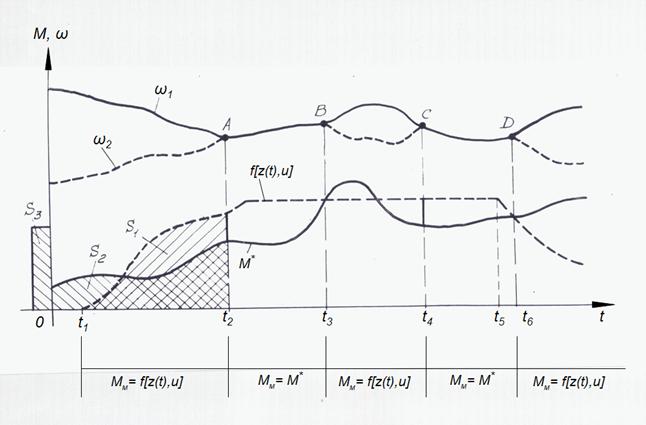
Рис. 6. Геометрическая интерпретация режима блокировки муфты.
При
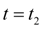 имеет место равенство площадей под кривыми моментов (45), т.е.
имеет место равенство площадей под кривыми моментов (45), т.е.
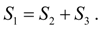 Это одновременно означает выравнивание угловых скоростей
Это одновременно означает выравнивание угловых скоростей
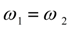 (точка А). В этот момент времени
(точка А). В этот момент времени
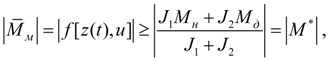 (46)
(46)
Поэтому произойдет скачок момента
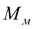 с
с
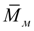 до
до
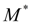 и дальнейшее движение полумуфт на промежутке
и дальнейшее движение полумуфт на промежутке
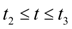 будет блокированным. При
будет блокированным. При
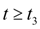 из-за увеличения
из-за увеличения
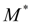 наступает момент, при котором
наступает момент, при котором
 (47)
(47)
и
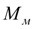 с точностью до знака становится равным
с точностью до знака становится равным
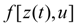 :
:
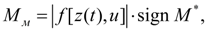 т.е. начинается пробуксовка муфты (
т.е. начинается пробуксовка муфты (
 , точка В).
, точка В).
При
 величина момента
величина момента
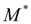 падает до значения, при котором вновь имеет место равенство
падает до значения, при котором вновь имеет место равенство
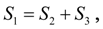 т.е.
т.е.
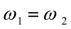 (точка С). Поскольку в этот момент времени опять выполняется условие (46), происходит новый скачок
(точка С). Поскольку в этот момент времени опять выполняется условие (46), происходит новый скачок
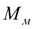 до значения
до значения
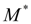 и на промежутке
и на промежутке
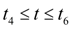 муфта снова блокируется. При
муфта снова блокируется. При
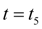 начинается принудительное размыкание муфты, предельный момент
начинается принудительное размыкание муфты, предельный момент
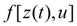 снижается, и при
снижается, и при
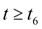 вновь становится меньше по модулю, чем
вновь становится меньше по модулю, чем
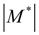 . В результате при
. В результате при
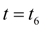 (точка D) снова начинается пробуксовка муфты.
(точка D) снова начинается пробуксовка муфты.
Условия блокировки (46) – (47) были учтены при записи математических моделей фрикциона (15) и гидротрансформатора (19) – (20).
Для гидротрансформатора с обгонной муфтой всегда
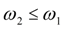 и блокировка наступает при
и блокировка наступает при
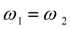 , поэтому условия блокировки насосного и турбинного колес гидротрансформатора (19) имеют некоторые формальные отличия от условий блокировки фрикциона (15).
, поэтому условия блокировки насосного и турбинного колес гидротрансформатора (19) имеют некоторые формальные отличия от условий блокировки фрикциона (15).
|
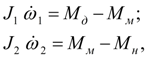 (36)
(36)
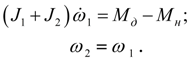 (37)
(37)
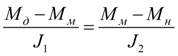 , (38)
, (38)
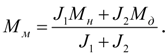 (39)
(39)
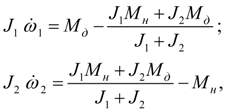 (40)
(40)
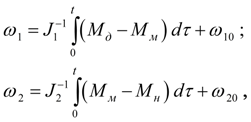 (42)
(42)
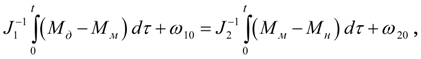 (43)
(43)
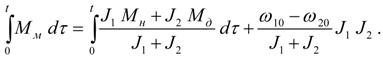 (44)
(44)
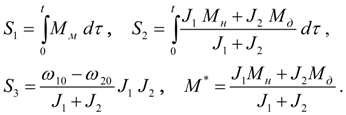 (45)
(45)

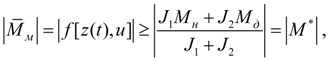 (46)
(46)