Приводы и трансмиссии - Библиотека базовых элементов и их математических моделей
Библиотека базовых элементов и их математических моделей
Вид уравнений базовых элементов всегда зависит от допущений, принимаемых при решении конкретных задач. Поскольку в данном случае рассматриваются методы
автоматизированного
динамического расчета, характеризующегося двумя основными особенностями: автоматическим формированием математической модели путем выбора нужных уравнений из общей библиотеки математических моделей и построением на основе этого программ массового пользования, рассчитанных на применение к приводам произвольного вида, необходимо было выбрать из большого числа имеющихся наиболее употребительные модели элементов, приемлемые для решения как можно более широкого круга задач. В результате для описания базовых элементов механических и гидромеханических передач были приняты приведенные ниже математические модели, в которых использованы следующие обозначения:
v
– линейная скорость;
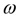 – угловая скорость;
z
–
линейное перемещение;
– угловая скорость;
z
–
линейное перемещение;
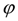 – угол поворота;
R
– сила;
М
– крутящий момент. Индексация переменных величин производится по номерам узлов, в которых действует данная переменная (рис. 1).
– угол поворота;
R
– сила;
М
– крутящий момент. Индексация переменных величин производится по номерам узлов, в которых действует данная переменная (рис. 1).
Приведенная ниже библиотека уравнений типовых элементов в принципе может допускать их различное математическое описание при условии сохранения концепции трехузлового элемента.
Приведенные на рис. 3 характеристики элементов механических и гидромеханических приводов аппроксимируются конечным набором точек
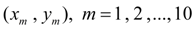 , где
х
– аргумент,
у
– функция, и задаются в табличной форме. Для получения текущего значения
у
(
х
) используется метод
линейной интерполяции
.
, где
х
– аргумент,
у
– функция, и задаются в табличной форме. Для получения текущего значения
у
(
х
) используется метод
линейной интерполяции
.
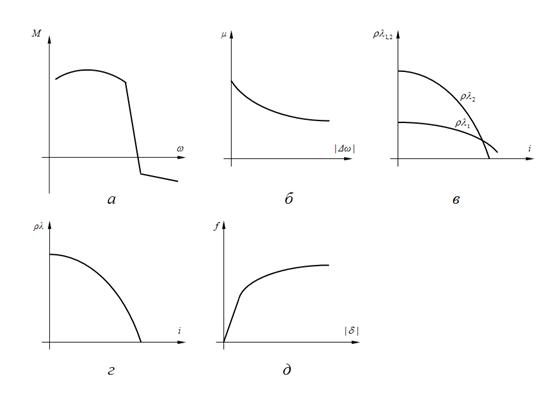
Рис. 3. Характеристики базовых элементов механических и гидромеханических передач:
а
– дизеля;
б
– фрикционной муфты;
в
– гидротрансформатора;
г
– гидромуфты;
д
– колеса (кривая буксования).
Дизель с центробежным регулятором.
Дизель с центробежным регулятором описывается уравнением моментов на валу (узел
j
) и уравнением движения муфты регулятора (узел
k
) [1, 2]:
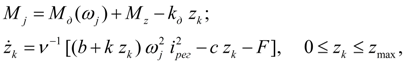 (9)
(9)
где
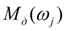 – характеристика дизеля при минимальной подаче топлива (рис. 3
а
) с учетом тормозной ветви, аппроксимируемая конечным набором точек
– характеристика дизеля при минимальной подаче топлива (рис. 3
а
) с учетом тормозной ветви, аппроксимируемая конечным набором точек
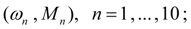
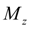 – приращение крутящего момента при максимальной подаче топлива;
– приращение крутящего момента при максимальной подаче топлива;
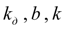 – постоянные настройки регулятора дизеля;
– постоянные настройки регулятора дизеля;
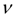 – коэффициент вязкого трения в регуляторе дизеля;
– коэффициент вязкого трения в регуляторе дизеля;
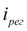 – передаточное отношение привода регулятора;
с
,
F
– жесткость и сила предварительного сжатия пружины;
– передаточное отношение привода регулятора;
с
,
F
– жесткость и сила предварительного сжатия пружины;
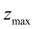 – максимальный ход муфты регулятора.
– максимальный ход муфты регулятора.
При моделировании переходных процессов часто бывает необходимо перейти в область частичных (регуляторных) характеристик дизеля, что в реальных условиях обеспечивается изменением величины
F
–силы предварительного сжатия пружины, регулируемой водителем с помощью рычага управления. В общем случае величина
F
меняется от нуля до максимума
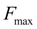 :
:
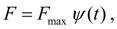 (10)
(10)
где
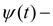 функция регулирования силы предварительного сжатия пружины,
функция регулирования силы предварительного сжатия пружины,
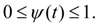
Редуктор.
В редукторе (рис. 1) имеет место постоянство передаточных чисел в узлах
i
,
j
,
k
, т.е.
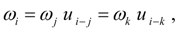 (11)
(11)
где
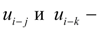 передаточные числа ветвей редуктора
передаточные числа ветвей редуктора
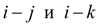 .
.
Пусть
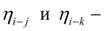 КПД редуктора в ветвях
КПД редуктора в ветвях
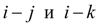 ; тогда суммарные потери на трение в редукторе, приведенные к узлу
i
, можно определить как
; тогда суммарные потери на трение в редукторе, приведенные к узлу
i
, можно определить как
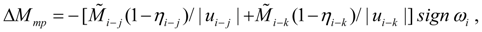 (12)
(12)
где
 абсолютные значения номинальных моментов, передаваемых соответственно в ветвях
абсолютные значения номинальных моментов, передаваемых соответственно в ветвях
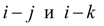 (в узлах
j
и
k
).
(в узлах
j
и
k
).
Упругий вал.
Момент кручения, развиваемый за счет упругой угловой деформации, зависящий также от демпфирующих свойств вала и приложенный в узле
j
(рис. 1), равен:
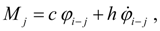 (13)
(13)
где
с
– угловая жесткость вала;
h
– коэффициент вязкого трения;
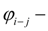 угол закручивания вала, определяемый уравнением:
угол закручивания вала, определяемый уравнением:
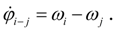 (14)
(14)
В узле
i
действует момент противоположного знака:
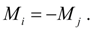
Фрикционная муфта.
Момент, реализуемый фрикционной муфтой и приложенный в узле
j
(рис. 1), равен [1, 2]:
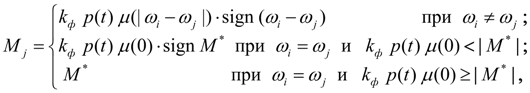 (15)
(15)
где
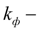 конструктивная постоянная фрикционной муфты;
конструктивная постоянная фрикционной муфты;
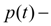 давление в механизме прижатия фрикционной пары в функции времени;
давление в механизме прижатия фрикционной пары в функции времени;
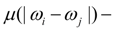 коэффициент трения в функции модуля относительной угловой скорости (рис. 3
б
);
коэффициент трения в функции модуля относительной угловой скорости (рис. 3
б
);
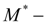 момент, реализуемый фрикционной муфтой при блокировке (подробно режим блокировки см. в разделе
«Блокировка фрикционных муфт и гидротрансформаторов»
).
момент, реализуемый фрикционной муфтой при блокировке (подробно режим блокировки см. в разделе
«Блокировка фрикционных муфт и гидротрансформаторов»
).
В узле
i
действует момент противоположного знака:
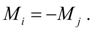
Гидротрансформатор.
Моменты, развиваемые на насосном (
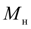 ) и турбинном (
) и турбинном (
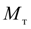 ) колесах гидротрансформатора [1, 2]:
) колесах гидротрансформатора [1, 2]:
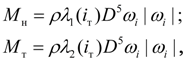 (16)
(16)
причем

Здесь
D
- активный диаметр рабочих колес гидротрансформатора,
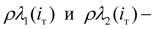 характеристики гидротрансформатора;
характеристики гидротрансформатора;
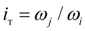 (рис. 3
в
);
(рис. 3
в
);
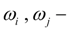 угловые скорости насосного (узел
i
) и турбинного (узел
j
) колес гидротрансформатора (рис. 3
е
).
угловые скорости насосного (узел
i
) и турбинного (узел
j
) колес гидротрансформатора (рис. 3
е
).
Коэффициент трансформации по определению равен:
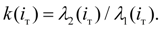 (17)
(17)
Тогда
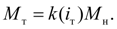 (18)
(18)
Если гидротрансформатор выполнен конструктивно с обгонной муфтой, то в режиме блокировки насосного (узел
i
) и турбинного (узел
j
) колес (подробно режим блокировки см. в разделе
«Блокировка фрикционных муфт и гидротрансформаторов»
) получим:
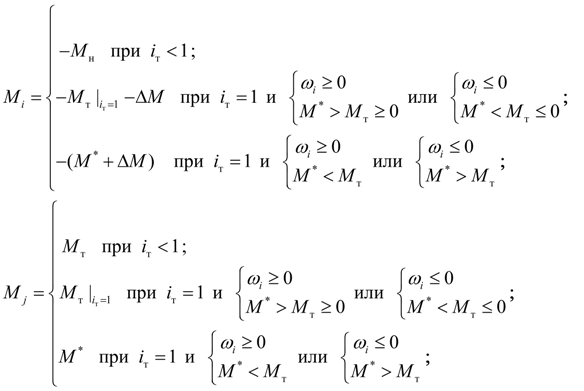 (19)
(19)
где
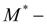 момент на турбинном колесе, определяемый из уравнений блокировки (см.
здесь
);
момент на турбинном колесе, определяемый из уравнений блокировки (см.
здесь
);
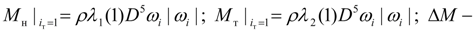 момент потерь на лопатках реактора:
момент потерь на лопатках реактора:
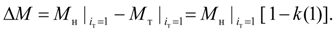
Если насосное и турбинное колеса гидротрансформатора блокируются фрикционом, то в режиме блокировки насосного (узел
i
) и турбинного (узел
j
) колес (подробно режим блокировки см. в разделе
«Блокировка фрикционных муфт и гидротрансформаторов»
) получим:
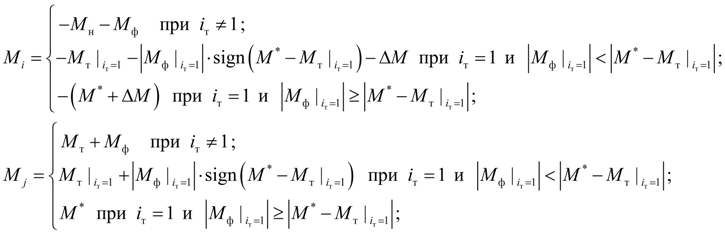 (20)
(20)
где
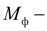 момент фрикционной муфты:
момент фрикционной муфты:
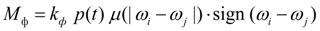 , (21)
, (21)
а при равенстве угловых скоростей
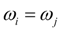
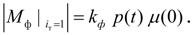 (22)
(22)
Гидромуфта.
Момент, реализуемый гидромуфтой:
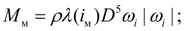 (23)
(23)
где
D
- активный диаметр рабочих колес гидромуфты,
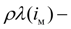 характеристика гидромуфты в функции
характеристика гидромуфты в функции
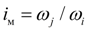 (рис. 3
г
).
(рис. 3
г
).
Поскольку при
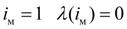 , то режима блокировки в гиромуфте нет, так как при равенстве угловых скоростей
, то режима блокировки в гиромуфте нет, так как при равенстве угловых скоростей
 момент, развиваемый гидромуфтой, равен нулю.
момент, развиваемый гидромуфтой, равен нулю.
Колесо (колесный движитель).
Для проведения тягово-динамических расчетов гидрообъемных трансмиссий самоходных колесных машин необходимо рассмотреть в качестве одного из базовых гидроэлементов колесо (колесный движитель) – рис. 1. На схеме индексами
i
,
j
,
k
обозначены соответственно узлы входа
i
(приводной вал колеса), выхода
j
(точка контакта колеса с дорогой) и перемещения машины
k
. Рассматриваемая здесь модель колесного движителя описывает жесткую связь колеса с гидромотором, т.е. возможные упругие деформации редуктора и вала между гидромотором и колесом не рассматриваются.
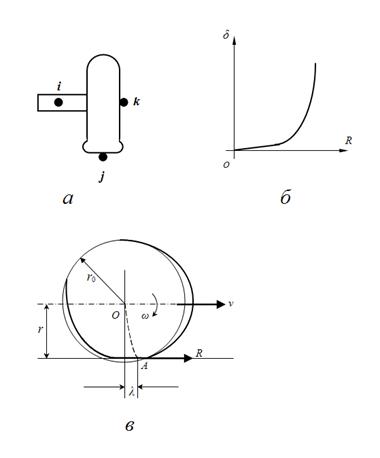
Рис. 4. К выводу уравнений динамики колеса.
С учетом принятых допущений математическая модель динамики колеса (колесного движителя), рис. 4, имеет вид [1, 2]:
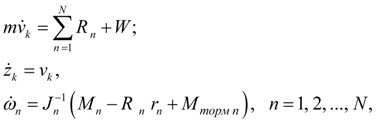 (24)
(24)
где
т
– масса машины;
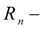 окружная сила в узле
j
(рис. 4) на
n
-ом колесе (на колесах
n
-ой оси);
W
– суммарная сила сопротивления перемещению машины;
окружная сила в узле
j
(рис. 4) на
n
-ом колесе (на колесах
n
-ой оси);
W
– суммарная сила сопротивления перемещению машины;
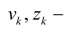 скорость и перемещение машины;
скорость и перемещение машины;
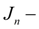 приведенный момент инерции вращающихся масс
n
-ой оси;
приведенный момент инерции вращающихся масс
n
-ой оси;
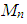 – активный момент
n
-ой оси;
– активный момент
n
-ой оси;
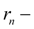 динамический радиус колеса (колес
n
-ой оси);
динамический радиус колеса (колес
n
-ой оси);
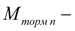 тормозной момент на валу
n
-ой оси, приложенный в начальном узле;
N
– число ведущих колес (осей).
тормозной момент на валу
n
-ой оси, приложенный в начальном узле;
N
– число ведущих колес (осей).
В установившемся режиме
окружная сила
R
на колесе связана с относительной пробуксовкой
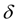 зависимостью [1, 4]:
зависимостью [1, 4]:
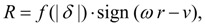 (25)
(25)
где
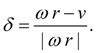 (26)
(26)
Здесь
ω
– угловая скорость колеса;
v
– скорость поступательного движения машины (узел
k
, рис. 1).
Величина динамического радиуса колеса
r
зависит от статического прогиба колеса под нагрузкой
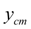 и динамического изменения прогиба колеса
y
(
t
) , зависящего от массы, приходящейся на ось, жесткости и демпфирования шин, неровностей профиля дороги. В нашем случае величину
y
(
t
) можно считать внешним воздействием. Тогда
и динамического изменения прогиба колеса
y
(
t
) , зависящего от массы, приходящейся на ось, жесткости и демпфирования шин, неровностей профиля дороги. В нашем случае величину
y
(
t
) можно считать внешним воздействием. Тогда
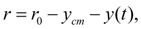 (27)
(27)
где
 – свободный радиус колеса;
– свободный радиус колеса;
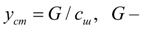 составляющая веса машины, приходящаяся на ось;
составляющая веса машины, приходящаяся на ось;
 радиальная жесткость шины.
радиальная жесткость шины.
В неустановившемся режиме
зависимось (25), имеющая статический характер, должна быть заменена динамической моделью. Для этого воспользуемся предложенной в [3] методикой, в соответствии с которой окружная сила
R
на колесе является функцией продольной деформации
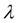 шины (рис. 4), а также сжатия набегающих волокон. После ряда преобразований [2] окончательно получим динамическую модель окружной силы
R
на колесе:
шины (рис. 4), а также сжатия набегающих волокон. После ряда преобразований [2] окончательно получим динамическую модель окружной силы
R
на колесе:
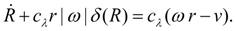 (28)
(28)
При установившемся режиме
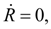 и тогда
и тогда
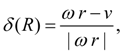 (29)
(29)
т.е. в установившемся режиме функция буксования
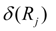 равна относительной пробуксовке колеса [ср. уравнения (28) – (29) с уравнениями (25) – (26)].
равна относительной пробуксовке колеса [ср. уравнения (28) – (29) с уравнениями (25) – (26)].
Таким образом, математическая модель колеса (колесного движителя) состоит из уравнений (24) и (28).
Дифференциал.
Дифференциал – это один из элементов, разделяющих схему на участки, для которых узлы
i
и
j
полуосей являются либо начальными (при разветвлении потока мощности), либо конечными (при суммировании потоков) – рис. 5.
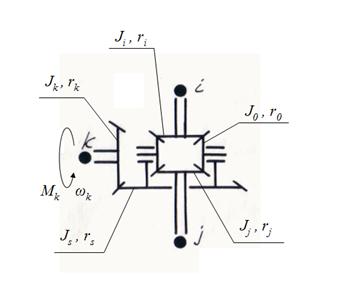
Рис. 5. Кинематическая схема дифференциала.
Угловые скорости полуосей связаны со скоростью входного вала следующей кинематической зависимостью:
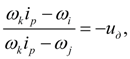 (30)
(30)
откуда
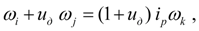 (31)
(31)
где
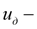 передаточное число дифференциала,
передаточное число дифференциала,
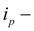 передаточное отношение редуктора между входным валом и водилом.
передаточное отношение редуктора между входным валом и водилом.
Для симметричного дифференциала
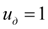 , и тогда
, и тогда
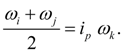 (32)
(32)
Моменты в узлах
i
,
j
,
k
(рис. 5) связаны соотношениями:
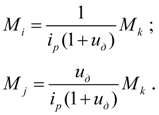 (33)
(33)
Тогда, зная момент
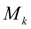 , легко определить моменты в узлах полуосей
, легко определить моменты в узлах полуосей
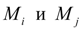 . С другой стороны, интегрируя уравнения динамики полуосей вида (2), получим
. С другой стороны, интегрируя уравнения динамики полуосей вида (2), получим
 , откуда, пользуясь уравнением (31), определим
, откуда, пользуясь уравнением (31), определим
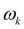 . Следовательно, необходимо определить величину
. Следовательно, необходимо определить величину
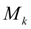 , для чего целесообразно входной вал дифференциала
всегда считать упругим
. Это означает, что узел
k
не может быть отнесен к какому-либо участку, что учтено в алгоритме
структурного анализа
, в результате которого узлы
i
и
j
являются либо начальными (если в схеме есть элементы, первые узлы которых совпадают с узлами
i
и
j
дифференциала), либо конечными (если в схеме есть элементы, вторые узлы которых совпадают с узлами
i
и
j
дифференциала), а узел
k
не входит ни в один из участков и
обязательно является узлом упругого вала
. Это не ограничивает общности решения задачи, зато позволяет сравнительно легко получить интересующие нас величины.
, для чего целесообразно входной вал дифференциала
всегда считать упругим
. Это означает, что узел
k
не может быть отнесен к какому-либо участку, что учтено в алгоритме
структурного анализа
, в результате которого узлы
i
и
j
являются либо начальными (если в схеме есть элементы, первые узлы которых совпадают с узлами
i
и
j
дифференциала), либо конечными (если в схеме есть элементы, вторые узлы которых совпадают с узлами
i
и
j
дифференциала), а узел
k
не входит ни в один из участков и
обязательно является узлом упругого вала
. Это не ограничивает общности решения задачи, зато позволяет сравнительно легко получить интересующие нас величины.
Запишем уравнения динамики полуосей дифференциала с учетом его геометрии, кинематики и действующих сил и моментов (рис. 5).
Исходные предпосылки и основная идея вывода этих уравнений принадлежат Л.Б.Зарецкому. Введем ряд дополнительных обозначений:
 тангенциальные силы взаимодействия в зубчатых зацеплениях входного редуктора и дифференциала;
тангенциальные силы взаимодействия в зубчатых зацеплениях входного редуктора и дифференциала;
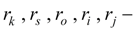 радиусы зацеплений зубчатых колес редуктора и дифференциала;
радиусы зацеплений зубчатых колес редуктора и дифференциала;
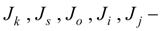 собственные моменты инерции зубчатых колес редуктора и дифференциала;
собственные моменты инерции зубчатых колес редуктора и дифференциала;
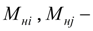 моменты нагрузки, приведенные к узлам
i
и
j
полуосей. Тогда динамику дифференциала можно описать следующей системой уравнений:
моменты нагрузки, приведенные к узлам
i
и
j
полуосей. Тогда динамику дифференциала можно описать следующей системой уравнений:
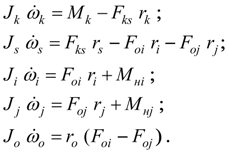 (34)
(34)
Учитывая, что
 , а также считая
, а также считая
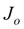 достаточно малым
достаточно малым
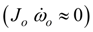 , после ряда простых алгебраических преобразований, исключив
, после ряда простых алгебраических преобразований, исключив
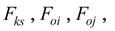 окончательно получим:
окончательно получим:
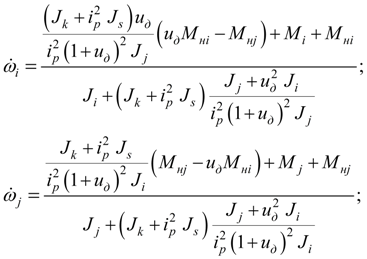 (35)
(35)
Таким образом, математическая модель дифференциала состоит из уравнений (31), (33) и (35).
|

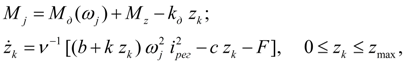 (9)
(9)
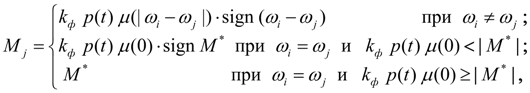 (15)
(15)
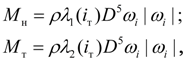 (16)
(16)
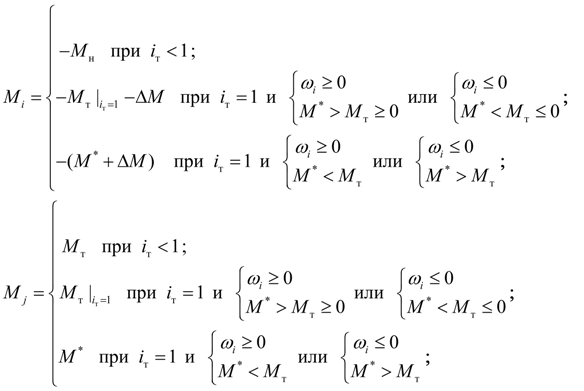 (19)
(19)
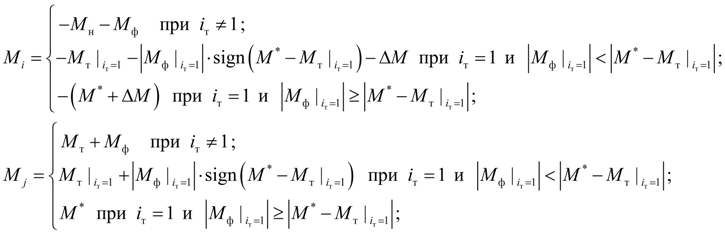 (20)
(20)

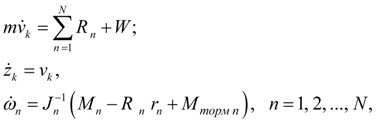 (24)
(24)
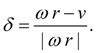 (26)
(26)
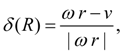 (29)
(29)

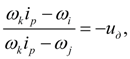 (30)
(30)
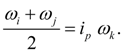 (32)
(32)
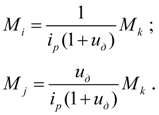 (33)
(33)
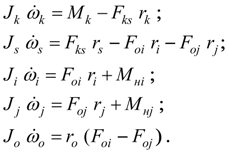 (34)
(34)
 , а также считая
, а также считая
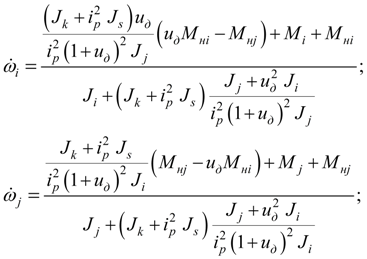 (35)
(35)