Динамический экспресс анализ гидросистем - Библиотека математических моделей функциональных блоков
Библиотека математических моделей функциональных блоков
Приведенные здесь математические модели функциональных блоков получены, исходя из следующих допущений:
- описание гидроэлементов, имеющих высокие собственные частоты (клапаны различных типов),
производится только на уровне их статических характеристик;
- анализ режимов течения рабочей жидкости (ламинарный или турбулентный) для определения
коэффициентов гидравлического сопротивления трубопроводов не производится; потери
давления по длине учитываются по формулам квадратичного сопротивления при
фиксированных (заданных) значениях приведенных коэффициентов гидравлического
сопротивления трубопроводов;
- приведение модуля упругости полости с рабочей жидкостью с учетом упругих свойств стенок
не производится, эта величина задается в числе исходных данных для каждого функционального
блока гидросхемы.
Эти допущения определяют в основном степень упрощения математических моделей для динамического экспресс-анализа по сравнению с более точным математическим описанием гидроэлементов, приведенным выше в разделе «
Динамический анализ гидросистем
» [1 - 3].
Дизель с центробежным регулятором.
Для описания динамики дизеля с центробежным регулятором (рис. 1
а
) достаточно записать уравнение моментов на валу (узел
k
) и уравнение движения муфты регулятора (узел
l
):
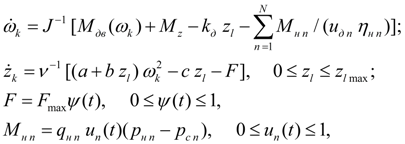 (1)
(1)
где
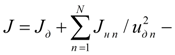 приведенный момент инерции, складывающийся из собственного момента инерции вращающихся частей дизеля
приведенный момент инерции, складывающийся из собственного момента инерции вращающихся частей дизеля
 и моментов инерции насосов
и моментов инерции насосов
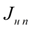 ;
;
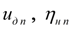 – передаточное число согласующего редуктора между дизелем и
n
-м насосом и механический КПД
n
-го насоса;
– передаточное число согласующего редуктора между дизелем и
n
-м насосом и механический КПД
n
-го насоса;
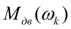 – характеристика дизеля (зависимость момента
– характеристика дизеля (зависимость момента
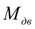 при минимальной подаче топлива от угловой скорости
при минимальной подаче топлива от угловой скорости
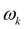 вала в узле
k
, аппроксимируемая конечным набором точек
вала в узле
k
, аппроксимируемая конечным набором точек

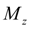 – приращение крутящего момента при максимальной подаче топлива;
– приращение крутящего момента при максимальной подаче топлива;
 – постоянные настройки центробежного регулятора дизеля;
– постоянные настройки центробежного регулятора дизеля;
 – коэффициент вязкого трения;
с
,
F
– жесткость и сила предварительного сжатия пружины регулятора,
– коэффициент вязкого трения;
с
,
F
– жесткость и сила предварительного сжатия пружины регулятора,
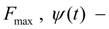 максимальная сила предварительного сжатия пружины и параметр ее регулирования (
максимальная сила предварительного сжатия пружины и параметр ее регулирования (
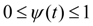 );
);
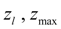 – текущее и максимальное перемещение муфты регулятора;
– текущее и максимальное перемещение муфты регулятора;
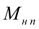 – нагрузочный момент двигателя со стороны
n
-го насоса,
– нагрузочный момент двигателя со стороны
n
-го насоса,
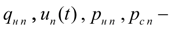 параметры
n
-го насоса:
параметры
n
-го насоса:
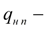 максимальный рабочий объем насоса,
максимальный рабочий объем насоса,
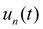 – параметр регулирования (
– параметр регулирования (
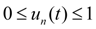 ),
),
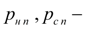 давления в напорной и сливной линиях насоса.
давления в напорной и сливной линиях насоса.
Насосная установка с разомкнутой циркуляцией потока.
В соответствии с расчетной схемой (рис. 2)
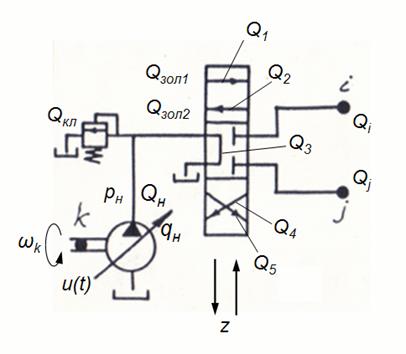
Рис. 2. Расчетная схема насосной установки с разомкнутой циркуляцией потока.
и принятыми выше допущениями математическая модель насосной установки с разомкнутой циркуляцией потока может быть записана в виде :
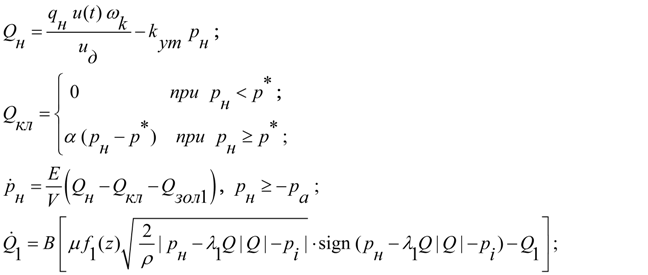 (2)
(2)
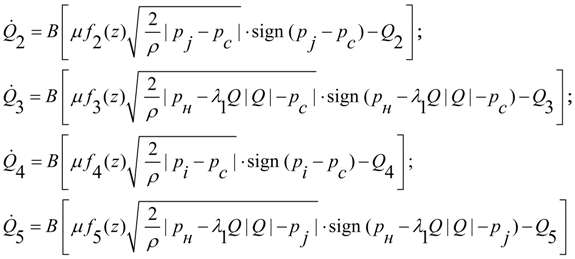
где
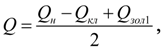
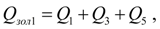
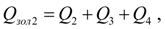
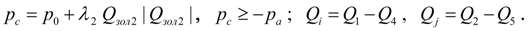
В уравнениях (2), описывающих динамику насосной установки с разомкнутой циркуляцией потока обозначено:
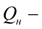 подача насоса;
подача насоса;
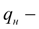 максимальный рабочий объем насоса;
максимальный рабочий объем насоса;
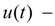 параметр регулирования подачи насоса
параметр регулирования подачи насоса
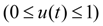 ;
;
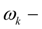 угловая скорость вала двигателя;
угловая скорость вала двигателя;
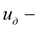 передаточное число согласующего редуктора между двигателем и насосом;
передаточное число согласующего редуктора между двигателем и насосом;
 коэффициент утечек (объемных потерь) насоса;
коэффициент утечек (объемных потерь) насоса;
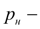 давление на выходе насоса;
р
* – давление срабатывания предохранительного клапана;
давление на выходе насоса;
р
* – давление срабатывания предохранительного клапана;
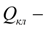 расход через предохранительный клапан;
α
– угловой коэффициент статической характеристики клапана
расход через предохранительный клапан;
α
– угловой коэффициент статической характеристики клапана
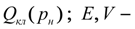 приведенный модуль упругости и объем полостей с жидкостью;
приведенный модуль упругости и объем полостей с жидкостью;
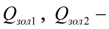 расходы жидкости в напорной и сливной гидролиниях золотникового распределителя;
расходы жидкости в напорной и сливной гидролиниях золотникового распределителя;
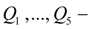 расходы жидкости в каналах распределителя;
μ
– коэффициент расхода каналов распределителя;
расходы жидкости в каналах распределителя;
μ
– коэффициент расхода каналов распределителя;
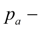 атмосферное давление;
атмосферное давление;
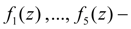 площади проходных сечений каналов распределителя в функции перемещения золотника;
ρ
– плотность рабочей жидкости;
площади проходных сечений каналов распределителя в функции перемещения золотника;
ρ
– плотность рабочей жидкости;
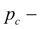 давление в начале сливной линии распределителя;
давление в начале сливной линии распределителя;
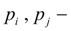 давления в магистралях за распределителем (узлы
i
и
j
) ;
давления в магистралях за распределителем (узлы
i
и
j
) ;
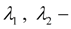 приведенные коэффициенты потерь давления с учетом гидравлических сопротивлений и геометрии трубопроводов;
приведенные коэффициенты потерь давления с учетом гидравлических сопротивлений и геометрии трубопроводов;
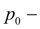 давление в гидробаке;
давление в гидробаке;
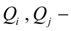 расходы жидкости в узлах
i
и
j
;
В
– параметр, учитывающий инерционные эффекты дросселирующих щелей гидрораспределителя [1].
расходы жидкости в узлах
i
и
j
;
В
– параметр, учитывающий инерционные эффекты дросселирующих щелей гидрораспределителя [1].
Насосная установка с замкнутой циркуляцией потока.
Согласно расчетной схеме насосной установки с замкнутой циркуляцией потока (рис. 3)
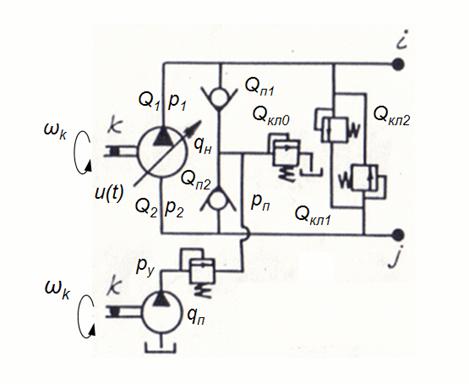
Рис. 3. Расчетная схема насосной установки с замкнутой циркуляцией потока.
и принятым выше допущениям математическая модель насосной установки этого типа имеет вид:
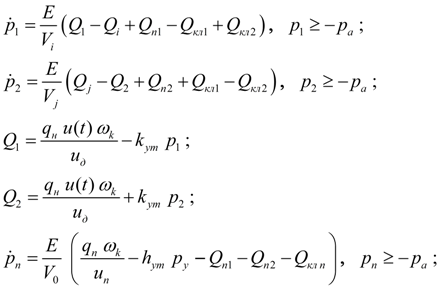
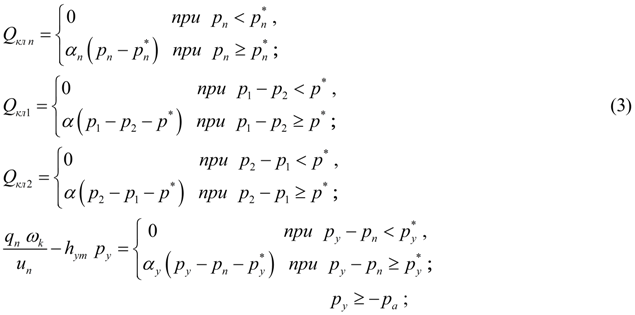
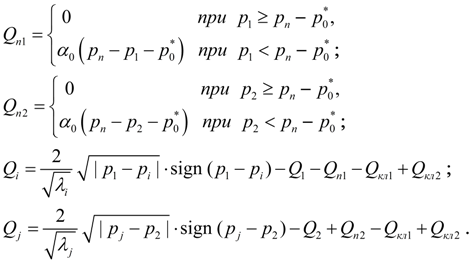
В уравнениях (3) приняты следующие обозначения:
 давления и расходы на выходе и входе основного насоса соответственно (рис. 3);
Е
– приведенный модуль упругости полостей с жидкостью;
давления и расходы на выходе и входе основного насоса соответственно (рис. 3);
Е
– приведенный модуль упругости полостей с жидкостью;
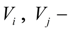 объемы полостей;
объемы полостей;
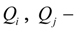 расходы в узлах
i
и
j
;
расходы в узлах
i
и
j
;
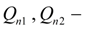 расходы подпитки через обратные клапаны;
расходы подпитки через обратные клапаны;
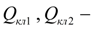 расходы через предохранительные клапаны;
расходы через предохранительные клапаны;
 максимальный рабочий объем основного насоса;
максимальный рабочий объем основного насоса;
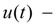 параметр регулирования подачи насоса
параметр регулирования подачи насоса
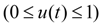 ;
;
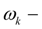 угловая скорость вала двигателя;
угловая скорость вала двигателя;
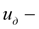 передаточное число согласующего редуктора между двигателем и насосом;
передаточное число согласующего редуктора между двигателем и насосом;
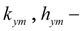 коэффициенты утечек (объемных потерь) в основном насосе и насосе подпитки;
коэффициенты утечек (объемных потерь) в основном насосе и насосе подпитки;
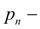 давление в системе подпитки перед обратными клапанами;
давление в системе подпитки перед обратными клапанами;
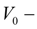 объем межклапанной полости в системе подпитки;
объем межклапанной полости в системе подпитки;
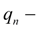 рабочий объем насоса подпитки;
рабочий объем насоса подпитки;
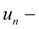 передаточное число согласующего редуктора между двигателем и насосом подпитки;
передаточное число согласующего редуктора между двигателем и насосом подпитки;
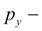 давление управления (на выходе насоса подпитки);
давление управления (на выходе насоса подпитки);
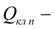 расход через предохранительный клапан системы подпитки;
расход через предохранительный клапан системы подпитки;
 угловые коэффициенты статических характеристик предохранительных клапанов основного контура и системы подпитки;
угловые коэффициенты статических характеристик предохранительных клапанов основного контура и системы подпитки;
 давления срабатывания предохранительных клапанов основного контура и системы подпитки;
давления срабатывания предохранительных клапанов основного контура и системы подпитки;
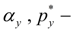 угловой коэффициент статической характеристики и давление срабатывания подпорного клапана;
угловой коэффициент статической характеристики и давление срабатывания подпорного клапана;
 угловой коэффициент статической характеристики и давление срабатывания обратного клапана;
угловой коэффициент статической характеристики и давление срабатывания обратного клапана;
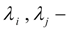 приведенные коэффициенты потерь давления по длине с учетом гидравлических сопротивлений и геометрии трубопроводов.
приведенные коэффициенты потерь давления по длине с учетом гидравлических сопротивлений и геометрии трубопроводов.
Гидромотор.
Динамика гидромотора с присоединенными напорным и сливным трубопроводами (расчетная схема – на рис. 4)
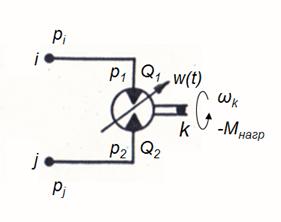
Рис. 4. Расчетная схема гидромотора.
с учетом принятых выше допущений может быть описана следующей системой дифференциально-алгебраических уравнений:
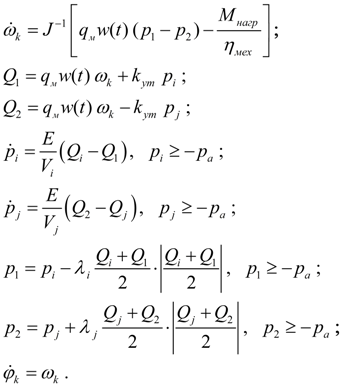 (4)
(4)
Два параллельно соединенных гидромотора.
Расчетная схема двух параллельно соединенных гидромоторов представлена на рис. 5,
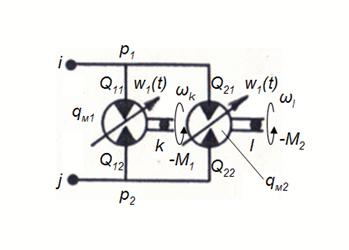
Рис. 5. Расчетная схема двух параллельно соединенных гидромоторов.
а математическая модель с учетом принятых допущений имеет вид:

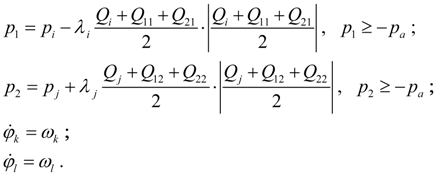
В уравнениях (4) и (5) обозначено:
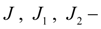 приведенные к валам гидромоторов моменты инерции вращающихся частей;
приведенные к валам гидромоторов моменты инерции вращающихся частей;
 максимальные рабочие объемы гидромоторов;
максимальные рабочие объемы гидромоторов;
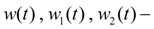 параметры регулирования рабочих объемов
параметры регулирования рабочих объемов
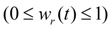 ;
;
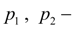 давления на входе и выходе гидромоторов;
давления на входе и выходе гидромоторов;
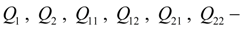 расходы на входе и выходе гидромоторов;
расходы на входе и выходе гидромоторов;
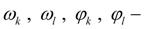 угловые скорости и углы поворота валов гидромоторов (в узлах
k
и
l
);
угловые скорости и углы поворота валов гидромоторов (в узлах
k
и
l
);
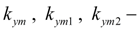 коэффициенты объемных потерь (утечек);
коэффициенты объемных потерь (утечек);
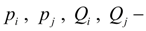 давления и расходы в узлах
i
и
j
;
Е
– приведенный модуль упругости полости с жидкостью;
давления и расходы в узлах
i
и
j
;
Е
– приведенный модуль упругости полости с жидкостью;
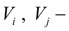 объемы полостей, примыкающих к узлам
i
и
j
;
объемы полостей, примыкающих к узлам
i
и
j
;
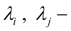 приведенные коэффициенты потерь давления по длине с учетом гидравлических сопротивлений и геометрии трубопроводов;
приведенные коэффициенты потерь давления по длине с учетом гидравлических сопротивлений и геометрии трубопроводов;
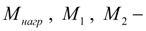 нагрузочные моменты, приведенные к валам гидромоторов с учетом КПД механизмов
нагрузочные моменты, приведенные к валам гидромоторов с учетом КПД механизмов
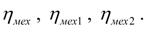
Гидроцилиндр.
Динамика гидроцилиндра с присоединенными напорной и сливной магистралями (расчетная схема – на рис. 6)
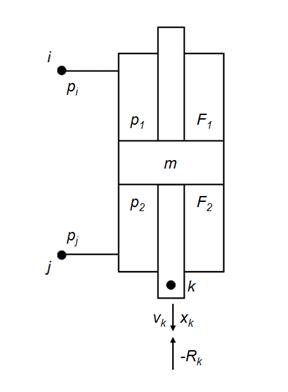
Рис. 6. Расчетная схема гидроцилиндра.
с учетом принятых допущений может быть описана следующей системой уравнений:
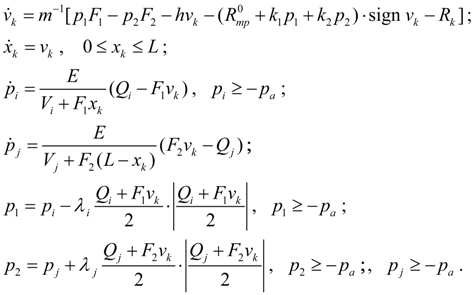 (6)
(6)
Два параллельно соединенных гидроцилиндра.
Математическая модель двух параллельно соединенных гидроцилиндров (расчетная схема представлена на рис. 7)
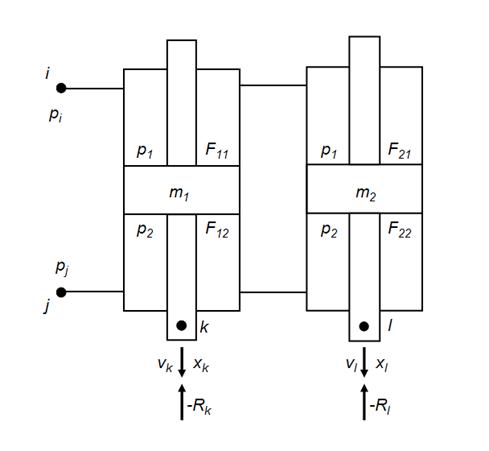
Рис. 7. Расчетная схема двух параллельно соединенных гидроцилиндров.
с учетом принятых допущений имеет вид:
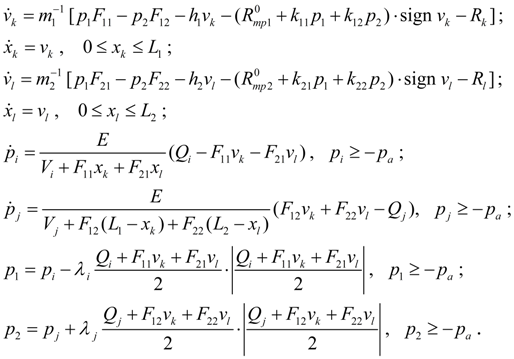 (7)
(7)
В уравнениях (6) – (7) приняты обозначения:
 приведеннные к штокам массы подвижных частей;
приведеннные к штокам массы подвижных частей;
 давления в полостях гидроцилиндров, примыкающих к узлам
i
и
j
;
давления в полостях гидроцилиндров, примыкающих к узлам
i
и
j
;
 рабочие площади поршней в полостях гидроцилиндров;
рабочие площади поршней в полостях гидроцилиндров;
 коэффициенты вязкого трения;
коэффициенты вязкого трения;
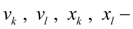 скорости и перемещения штоков гидроцилиндров (узлы
k
и
l
);
скорости и перемещения штоков гидроцилиндров (узлы
k
и
l
);
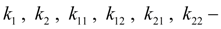 коэффициенты пропорциональности между давлениями в полостях гидроцилиндров и силами трения в уплотнениях;
коэффициенты пропорциональности между давлениями в полостях гидроцилиндров и силами трения в уплотнениях;
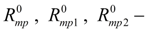 значения сил трения в уплотнениях при отсутствии давления;
значения сил трения в уплотнениях при отсутствии давления;
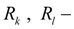 внешние усилия на штоках гидроцилиндров (узлы
k
и
l
);
внешние усилия на штоках гидроцилиндров (узлы
k
и
l
);
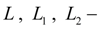 значения максимального перемещения (хода) поршней;
значения максимального перемещения (хода) поршней;
 давления в узлах
i
и
j
трубопроводов, примыкающих к полостям гидроцилиндров;
Е
– приведенный модуль упругости полостей с жидкостью;
давления в узлах
i
и
j
трубопроводов, примыкающих к полостям гидроцилиндров;
Е
– приведенный модуль упругости полостей с жидкостью;
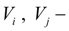 минимальные объемы полостей и примыкающих к узлам
i
и
j
трубопроводов;
минимальные объемы полостей и примыкающих к узлам
i
и
j
трубопроводов;
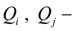 расходы в узлах
i
и
j
;
расходы в узлах
i
и
j
;
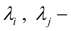 приведенные коэффициенты потерь давления по длине с учетом гидравлических сопротивлений и геометрии трубопроводов.
приведенные коэффициенты потерь давления по длине с учетом гидравлических сопротивлений и геометрии трубопроводов.
Упруго-инерционная нагрузка.
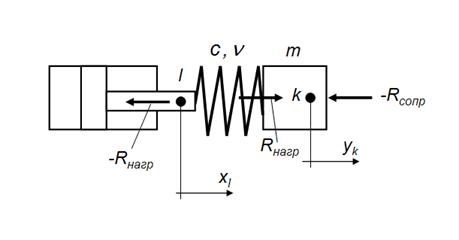
Рис. 8. Расчетная схема упруго-инерционной нагрузки при поступательном движении.
При поступательном движении
(рис. 8) упруго-инерционная нагрузка описывается уравнениями:
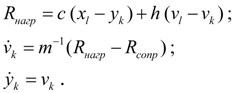 (8)
(8)
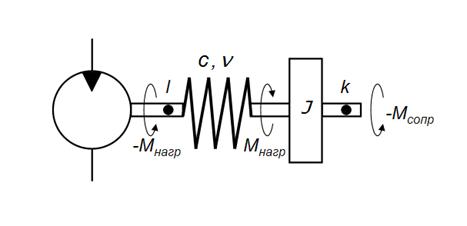
Рис. 9. Расчетная схема упруго-инерционной нагрузки при вращательномдвижении.
При вращательном движении
(рис. 9) упруго-инерционная нагрузка описывается уравнениями:
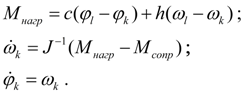 (9)
(9)
В уравнениях (8) и (9) приняты обозначения:
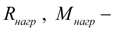 соответственно сила и момент нагрузки;
с
,
h
– жесткость и коэффициент вязкого трения;
соответственно сила и момент нагрузки;
с
,
h
– жесткость и коэффициент вязкого трения;
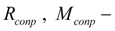 соответственно сила и момент сопротивления;
т
,
J
– масса и момент инерции нагрузки;
соответственно сила и момент сопротивления;
т
,
J
– масса и момент инерции нагрузки;
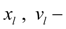 перемещение и скорость штока гидроцилиндра (узел
l
);
перемещение и скорость штока гидроцилиндра (узел
l
);
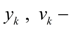 перемещение и скорость массы (узел
k
);
перемещение и скорость массы (узел
k
);
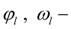 угол поворота и угловая скорость вала гидромотора (узел
l
);
угол поворота и угловая скорость вала гидромотора (узел
l
);
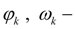 угол поворота и угловая скорость вращающейся массы (узел
k
).
угол поворота и угловая скорость вращающейся массы (узел
k
).
Колесный движитель (колесо).
Этот блок необходим при проведении тягово-динамических расчетов гидрообъемных трансмиссий самоходных колесных машин. Рассматриваемая здесь математическая модель колесного движителя описывает жесткую связь колеса с гидромотором (рис. 10
а
), т.е. возможные упругие деформации редуктора и вала между гидромотором и колесом не рассматриваются.
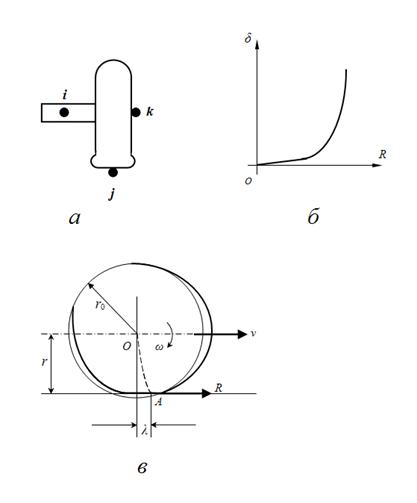
Рис. 10. Расчетная схема динамики колеса.
а
– гидромотор,
б
– кривая буксования,
в
– динамика колеса
С учетом принятых допущений математическая модель динамики колеса (колесного движителя), рис. 10
в
, имеет вид:
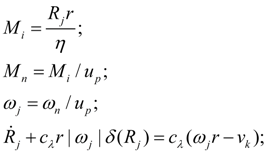 (10)
(10)
где
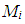 – момент на колесе с учетом потерь в редукторе;
– момент на колесе с учетом потерь в редукторе;
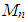 – момент, на валу гидромотора;
– момент, на валу гидромотора;
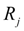 – тяговая реакция (окружная сила) на колесе;
r
– динамический радиус колеса;
– тяговая реакция (окружная сила) на колесе;
r
– динамический радиус колеса;
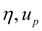 – КПД и передаточное число редуктора колеса;
– КПД и передаточное число редуктора колеса;
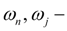 угловые скорости вала гидромотора и колеса;
угловые скорости вала гидромотора и колеса;
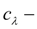 тангенциальная жесткость шины;
тангенциальная жесткость шины;
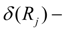 функция буксования (рис. 10
б
).
функция буксования (рис. 10
б
).
Машина.
Динамика поступательного движения машины описывается системой уравнений:
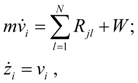 (11)
(11)
где
 масса, скорость, перемещение и суммарная сила сопротивления перемещению машины;
масса, скорость, перемещение и суммарная сила сопротивления перемещению машины;
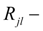 тяговая реакция (окружная сила) на
l
-ом ведущем колесе в узле
j
,
l
= 1, …,
N
;
N
– число ведущих колес (осей).
тяговая реакция (окружная сила) на
l
-ом ведущем колесе в узле
j
,
l
= 1, …,
N
;
N
– число ведущих колес (осей).
|
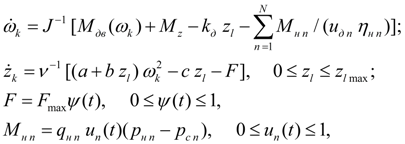 (1)
(1)
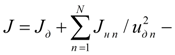 приведенный момент инерции, складывающийся из собственного момента инерции вращающихся частей дизеля
приведенный момент инерции, складывающийся из собственного момента инерции вращающихся частей дизеля

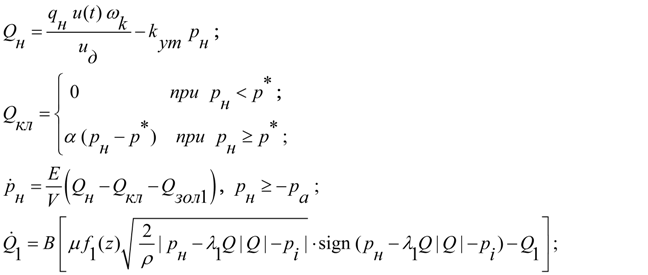 (2)
(2)
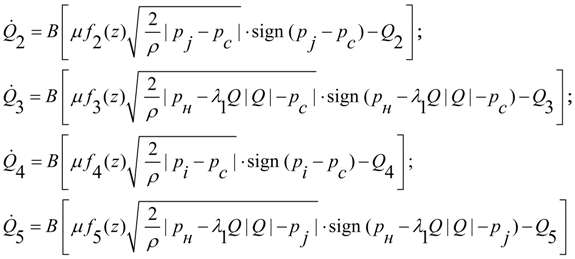
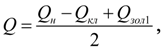

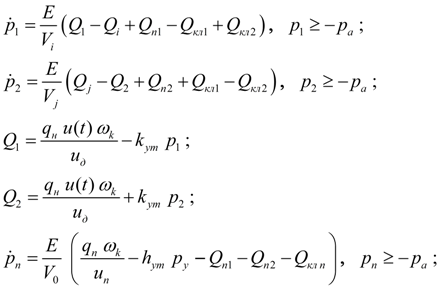
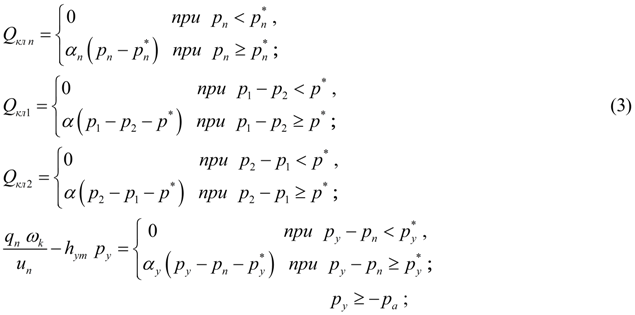
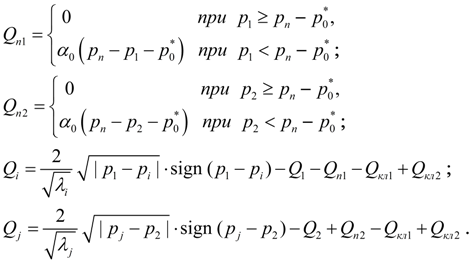

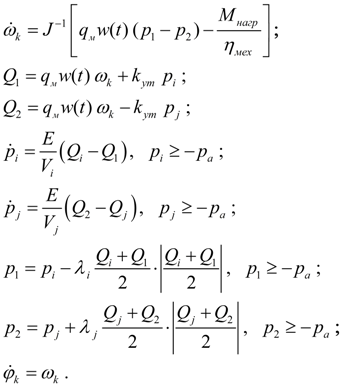 (4)
(4)


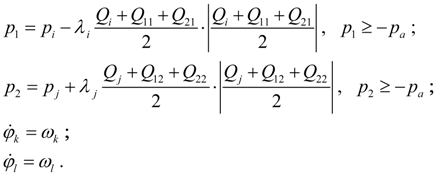

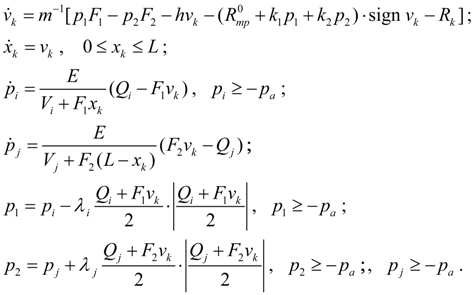 (6)
(6)

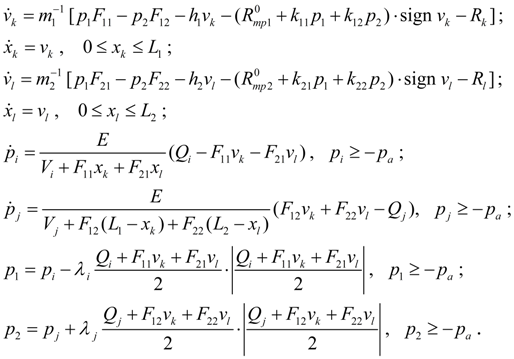 (7)
(7)

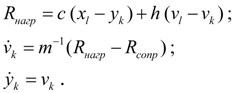 (8)
(8)

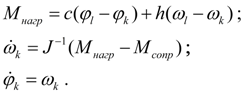 (9)
(9)

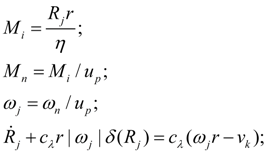 (10)
(10)
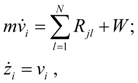 (11)
(11)