Библиотека гидроэлементов и их математических моделей
Вид уравнений базовых гидроэлементов зависит, вообще говоря, от допущений, принимаемых при решении конкретных задач. Поскольку в данном случае нами рассматриваются методы
автоматизированного
динамического расчета, характеризующегося двумя основными особенностями: автоматическим формированием математической модели путем выбора нужных уравнений из общей библиотеки математических моделей и построением на основе этого программ массового пользования, рассчитанных на применение к гидросистемам произвольного вида, необходимо было выбрать из большого числа имеющихся наиболее употребительные модели элементов, приемлемые для решения как можно более широкого круга задач. Поэтому для некоторых гидроэлементов, описываемых с различной степенью детализации (трубопровод, местные сопротивления), автором были проведены специальные исследования [1], целью которых был сравнительный анализ применяемых моделей для оценки степени их адекватности при различных внешних возмущениях и параметрах. В результате для описания гидроэлементов, выбранных в качестве базовых были приняты приведенные ниже математические модели, в которых введены следующие обозначения:
р
– давление;
Q
– подача или расход;
М
– крутящий момент. Индексация переменных величин производится по номерам узлов, в которых действует данная переменная (рис. 1).
Насос. Для описания насоса достаточно записать уравнение моментов на валу (узел k ) и уравнения потоков на входе (узел i ) и выходе (узел j ) с учетом объемных потерь. При этом неравномерность подачи насоса вследствие кинематических особенностей и сжимаемости жидкости в полостях всасывания и нагнетания не учитывается. С учетом принятых допущений математическая модель насоса имеет вид [1, 2]:
где
q
н
– максимальный рабочий объем насоса;
f
(
q
)
– параметр регулирования; – 1
≤
f
(
q
)
≤
1;
ω
в
– угловая скорость вала двигателя (дизеля);
а
ω
,
а
p
,
а
– коэффициенты гидромеханических потерь насоса, зависящих от угловой скорости, давления, и постоянная гидромеханических потерь;
u
д
– передаточное число редуктора между двигателем и насосом;
k
ут
– коэффициент объемных потерь насоса; для
Q
i
,
p
i
принимается знак «плюс», а для
Q
j
,
p
j
– «минус». Значения
а
ω
,
а
p
,
а
,
k
ут
выбирают по каталогу или из паспортных характеристик механического и объемного КПД насоса определенного типоразмера.
Гидромотор.
Математическая модель гидромотора должна отражать его динамику (уравнение моментов в узле
k
, разрешенное относительно углового ускорения и записанное в нормальной форме), а также уравнения потоков на входе (узел
i
) и выходе (узел
j
) с учетом объемных потерь.
где
ω
k
– угловая скорость вала гидромотора;
J
гм
– момент инерции гидромотора с учетом вращающихся масс рабочего механизма;
q
м
– максимальный рабочий объем гидромотора;
f
(
q
)
– параметр регулирования; – 1
≤
f
(
q
)
≤
1;
М
н
– нагрузочный момент;
b
ω
,
b
p
,
b
– коэффициенты гидромеханических потерь гидромотора, зависящих от угловой скорости, давления, и постоянная гидромеханических потерь;
u
мех
– передаточное число редуктора рабочего механизма;
k
ут
– коэффициент объемных потерь гидромотора; для
Q
i
,
p
i
принимается знак «плюс», а для
Q
j
,
p
j
– «минус».
Гидроцилиндр.
Динамика гидроцилиндра описывается уравнениями поступательного движения поршня (узел
k
) под действием сил давления, внешней нагрузки, сил трения и уравнениями расходов на входе (узел
i
) и выходе (узел
j
) с учетом сжимаемости жидкости в полостях цилиндра.
где
v
k
– скорость перемещения поршня;
т
– приведенная к штоку масса подвижных частей гидроцилиндра;
F
i
= π (
D
Коэффициенты пропорциональности между давлениями в полостях I (узел i ) и II (узел j ) и силой трения в манжетных уплотнениях: k i = π f ( D ц + D i ) H / 2, k j = π f ( D ц + D j ) H / 2, а коэффициенты упругости полостей с жидкостью:
k
где f – коэффициент трения уплотнения по поверхности цилиндра; H – высота манжетного уплотнения; ΔV i и ΔV j – мертвые объемы полостей I
и
II
;
E
E
здесь
Е
m
где P – движущая сила, то функция сухого трения f ( v k ) определится следующим образом [2]:
Такая модель трения отражает наличие зоны застоя при нулевой скорости подвижной части, например, при страгивании.
Трубопровод.
Для описания динамических процессов в трубопроводе с жидкостью использована математическая модель с сосредоточенными параметрами на входе (узел
i
) и выходе (узел
j
) трубопровода, справедливая при следующих условиях:
где
k
k
здесь
d
E
где
Е
здесь Re = 2 |
Qi
+
Qj
| / (
Тупиковый участок трубопровода (полость). Для тупикового участка трубопровода потерями давления по длине можно пренебречь, и тогда уравнения динамики принимают вид:
где
k
k
здесь
d
E
где
Е
Местное сопротивление (дроссель). Расход жидкости через дроссель связан с перепадом давления на входе (узел i ) и выходе (узел j ) известной зависимостью [1, 2]:
где
Использование уравнений расходов (9) часто служит причиной неустойчивости вычислительного процесса из-за стремления к бесконечности производной квадратного корня в нуле (это имеет место при малых перепадах давлений). Уравнение (9) определяет расход через дроссель в установившемся режиме течения жидкости и, следовательно, не учитывает инерционные свойства жидкости. Более точно зависимость расхода через дроссель выражается дифференциальным уравнением [3]:
где
l
– длина столба жидкости в местном сопротивлении; кроме того, для краткости записи здесь обозначено:
которое лишено указанных недостатков и асимптотическое решение которого совпадает с решением уравнения (9). Здесь
В
– параметр, учитывающий инерционность столба жидкости и зависящий от
l
и ряда других величин (
Тройник (делитель или сумматор потоков). Уравнения расходов в узлах i , j , k тройника при делении потока имеют вид [1, 2]:
где
Клапаны.
где
v
k
– скорость движения запорно-регулирующего элемента;
m
– масса подвижной части клапана;
F
i
и
F
j
– рабочие площади запорно-регулирующего элемента клапана со стороны напорной и сливной линии;
h
– коэффициент вязкого трения;
R
Приведенные уравнения относятся к предохранительному и обратному клапану. Соответствующие уравнения для редукционного клапана имеют незначительные отличия. В уравнениях (13) не учтена гидродинамическая сила, которая оказывает существенное влияние лишь на статическую характеристику клапана [2]. Клапан непрямого действия можно представить в виде двух элементов: основного клапана с узлами r , s , t и вспомогательного клапана с узлами i , j , k . Если узел j является общим для обоих клапанов, т.е. s = k , то математическая модель клапана непрямого действия имеет вид [1, 2]:
где
т
и
М
– массы подвижных частей вспомогательного и основного клапанов;
Гидроаккумулятор. Для описания динамики гидропневматического или пружинного аккумулятора необходимо записать уравнения движения поршня (мембраны) в узле k , уравнение давлений на входе (узел i ) и уравнение политропного процесса в газовой полости (узел j ) [1, 2]:
где
т
– масса подвижной части гидроаккумулятора;
F
=
здесь ΔV
E
здесь
Е
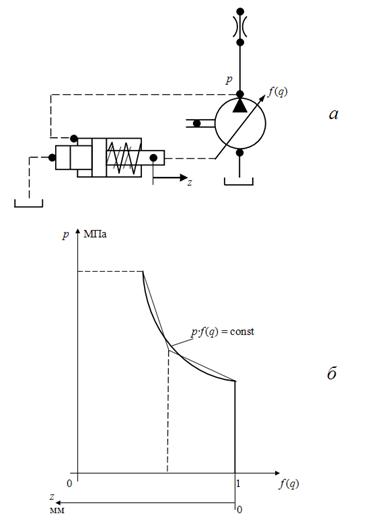
Регулятор мощности
предназначен для поддержания в определенном рабочем диапазоне насоса постоянства мощности, отбираемой от двигателя
pQ
= const. На самом деле, регулятор мощности обеспечивает постоянство величины:
p
f
(
q
)
= const. Однако, учитывая, что
Q
=
q
н
f
(
q
)
Тогда регулятор мощности описывается следующей системой уравнений [1, 2]:
где
т
– масса подвижной части регулятора;
А
– коэффициент, учитывающий для аксиально-поршневых насосов дополнительный момент, действующий на качающий узел;
F
– рабочая площадь плунжера под давлением каждой из двух магистралей;
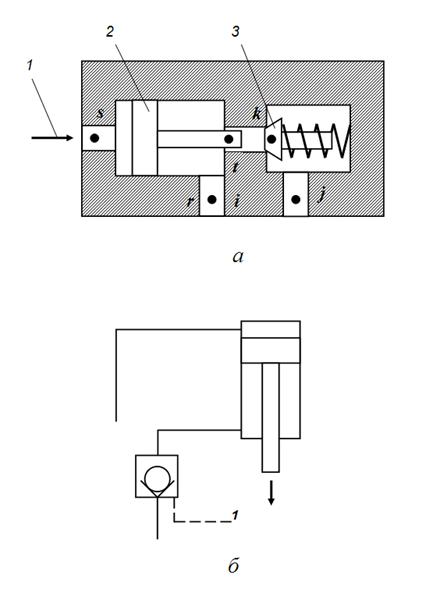
Гидрозамок.
Гидрозамки (или управляемые обратные клапаны) используются для фиксации и управления опусканием рабочих органов, находящихся под действием внешних нагрузок, в гидросистемах строительных машин (кранов, погрузчиков, грузовых лебедок). На рис. 3 показана расчетная схема гидрозамка и схема его подключения в гидросистеме. При подаче жидкости
1
в полость под клапаном
3
последний работает как обычный обратный клапан, пропуская поток рабочей жидкости к гидроцилиндру. При подаче жидкости
1
под поршень толкателя
2
последний принудительно открывает клапан, обеспечивая дросселирование потока на выходе гидроцилиндра при опускании поршня. На схеме индексами
i
,
j
,
k
обозначены узлы соответственно входа, выхода и перемещения клапана, а индексами
r
,
s
,
t
– узлы соответственно входа, выхода и перемещения толкателя. Гидрозамки выпускаются в двух модификациях: с общим дренажем толкателя и клапана (в этом случае
r
=
i
) и с раздельным дренажем ( тогда
r
В зависимости от того, находятся ли толкатель и клапан в контакте или нет, динамика гидрозамка описывается двумя различными математическими моделями. В момент возникновения контакта, когда толкатель начинает воздействовать на клапан, происходит их соударение, что приводит к необходимости коррекции координат состояния в соответствии с существующими зависимостями теории ударных систем.
где
т
и
М
– массы клапана и толкателя;
и при отсутствии удара оба тела перемещаются совместно, поэтому их движение описывается системой уравнений:
где х 0 – начальный зазор между толкателем и клапаном. Данная модель является неполной, так как, учитывая большие скорости и геометрию подвижных частей, соприкосновение которых можно рассматривать как центральный удар упругих стержней, было бы неверным считать, что при выполнении условий (18) система мгновенно переходит из состояния, описываемого уравнениями (17) в состояние, описываемое уравнениями (19). Этим объясняется необходимость введения модели переходного – ударного режима.
Для рассматриваемой ударной системы «толкатель-клапан» можно применить формулы классической гипотезы удара. Пусть до удара тело массой
т
имело скорость
где
Золотниковый распределитель. Гидрораспределитель представляет собой комплекс местных сопротивлений, образованных его каналами и связывающих примыкающие к ним узлы r и s . Расход через каждое такое местное сопротивление выражается уравнением, аналогичным уравнению (11):
где
где
i
, … ,
m
– номера узлов распределителя;
где
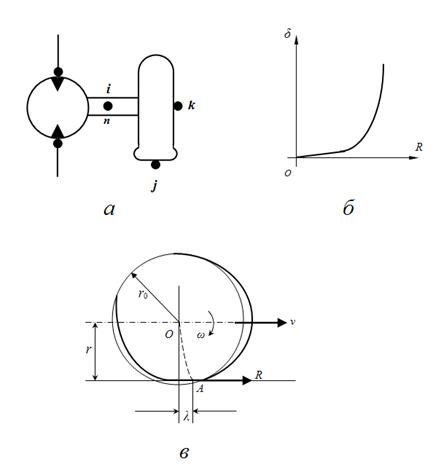
Колесо (колесный движитель). Для проведения тягово-динамических расчетов гидрообъемных трансмиссий самоходных колесных машин необходимо рассмотреть в качестве одного из базовых гидроэлементов колесо (колесный движитель) – рис. 1. На схеме индексами i , j , k обозначены соответственно узлы входа (приводной вал колеса), выхода (точка контакта колеса с дорогой) и перемещения машины. Рассматриваемая здесь модель колесного движителя описывает жесткую связь колеса с гидромотором, т.е. возможные упругие деформации редуктора и вала между гидромотором и колесом не рассматриваются.
а – расчетная схема, б – кривая буксования, в – деформация шины.
С учетом принятых допущений математическая модель динамики колеса (колесного движителя), рис. 5 а , имеет вид:
где
М
i
– момент на колесе с учетом потерь в редукторе;
М
n
– момент, приведенный к валу гидромотора;
В установившемся режиме
окружная сила
R
на колесе связана с относительной пробуксовкой
где
Здесь
ω
– угловая скорость колеса;
v
– скорость поступательного движения машины (узел
k
, рис. 1).
где
В неустановившемся режиме
зависимось (26), имеющая статический характер, должна быть заменена динамической моделью. Для этого воспользуемся предложенной в [5] методикой, в соответствии с которой окружная сила
R
на колесе является функцией продольной деформации
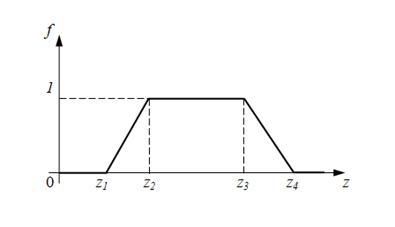
При установившемся режиме
т.е. в установившемся режиме функция буксования
Элементы систем управления (типовые линейные динамические звенья автоматического регулирования) . В системах управления объемным гидроприводом используются разнообразные физические устройства: гидравлические, электромагнитные, электрогидравлические и др. Поэтому при решении задач динамики гидросистем приходится моделировать различные по своей природе системы управления и регулирования. Большинство из них хорошо описывается с помощью типовых линейных динамических звеньев автоматического регулирования [7]. К ним относятся:
1) идеальное усилительное (безынерционное) звено – сумматор;
Математические модели перечисленных линейных динамических звеньев записаны далее в виде обыкновенных дифференциальных уравнений, а не в операторной форме (в виде передаточных функций), поскольку нас интересуют переходные процессы во временно’й, а не в частотной области.
В общем случае линейное динамическое звено 2-го порядка описывается уравнением:
где
Для всех остальных типов динамических звеньев их уравнения получены как частные случаи (31): идеальное усилительное (безынерционное) звено – сумматор:
апериодическое звено 1-го порядка (инерционное):
апериодическое звено 2-го порядка и колебательное звено:
консервативное звено:
идеальное интегрирующее звено:
инерциальное интегрирующее звено:
идеальное дифференцирующее звено:
идеальное звено с введением производной:
инерционное дифференцирующее звено:
Таким образом, все типовые линейные звенья могут быть объединены в один обобщенный элемент ЗВЕНО (идентификатор этого элемента в библиотеке базовых гидроэлементов) с узлами i (вход), j (выход), k (дополнительный вход для звена – сумматора). Учитывая специфику гидравлических систем, в правых частях уравнений динамических звеньев в качестве входных сигналов могут быть добавлены давления:
Условия, ограничения, комментарии. Приведенные математические модели гидроэлементов следует дополнить рядом ограничений, отражающих физические свойства переменных, а также некоторые конструктивные особенности устройств (например, упоры подвижных частей). Поскольку в уравнениях рассматривается избыточное давление, необходимо выполнение условий:
где
В ряде элементов (гидроцилиндр, клапан, регулятор мощности, дизель и др.) перемещение z подвижных частей ограничено упорами. Такого рода нелинейности могут быть заданы в виде неравенств:
где
L
– максимальное значение перемещения
z
;
А
– правая часть дифференциального уравнения, разрешенного относительно
|
Содержание
>> Инженерная математика
>> Гидравлические системы
>> Динамический анализ
>> Библиотека гидроэлементов и их математических моделей
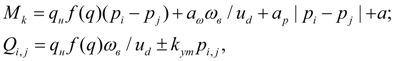 , (3)
, (3)
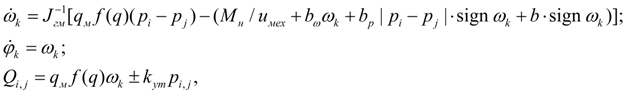 (4)
(4)
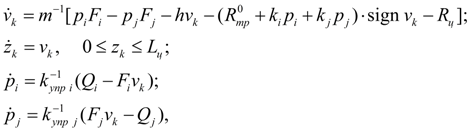 (5)
(5)
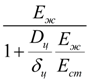 ,
,
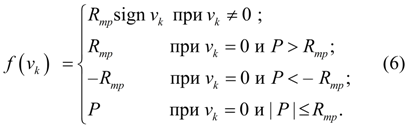
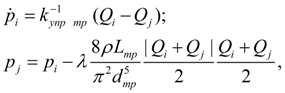 (7)
(7)
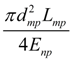 ,
,
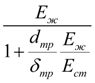 ,
,
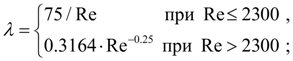
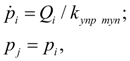 (8)
(8)
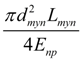 ,
,
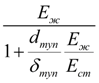 ,
,
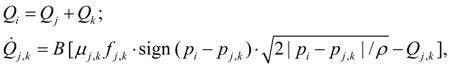 (12)
(12)
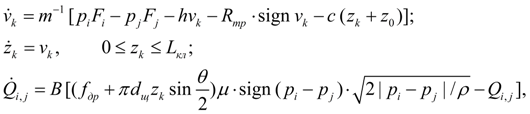 (13)
(13)
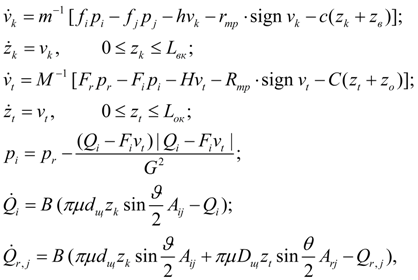 (14)
(14)
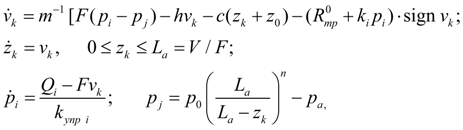 (15)
(15)
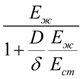 ,
,
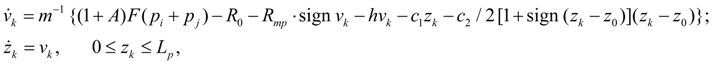 (16)
(16)
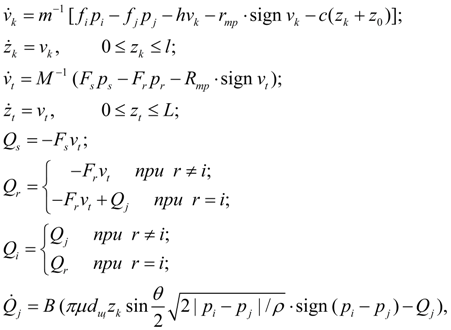 (17)
(17)
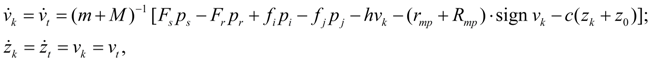 (19)
(19)
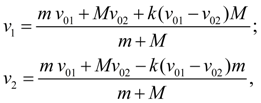 (20)
(20)
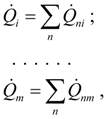 (22)
(22)
 (23)
(23)
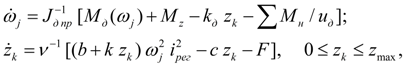 (24)
(24)
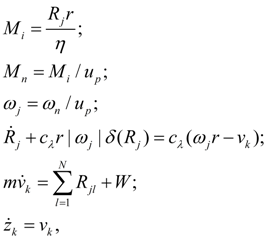 (25)
(25)
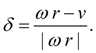 (27)
(27)
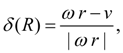 (30)
(30)
 (33)
(33)
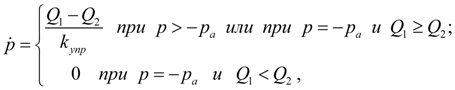 (34)
(34)
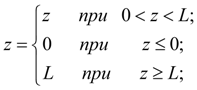 (35)
(35)
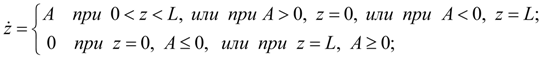 (36)
(36)
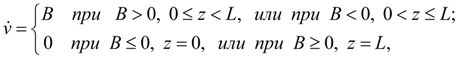 (37)
(37)