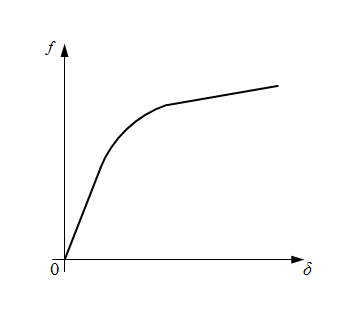Библиотека гидроэлементов и их математических моделей
Статический расчет
является основным этапом при проектировании гидравлических приводов и трансмиссий различных машин и механизмов. На основании результатов статического расчета осуществляется синтез гидросхемы и подбор элементов определенного типоразмера. Но в то же время он тесно связан с динамическим расчетом как предварительный этап, необходимый для корректного задания начального состояния гидросистемы при моделировании переходных процессов.
Насос. Для описания насоса достаточно записать уравнение моментов на валу (узел k ) и уравнения потоков на входе (узел i ) и выходе (узел j ) с учетом объемных потерь. При этом неравномерность подачи насоса вследствие кинематических особенностей и сжимаемости жидкости в полостях всасывания и нагнетания не учитывается. С учетом принятых допущений математическая модель насоса имеет вид [1, 2]:
где
q
н
– максимальный рабочий объем насоса;
f
(
q
)
– параметр регулирования; – 1
≤
f
(
q
)
≤
1;
ω
в
– угловая скорость вала двигателя (дизеля);
а
ω
,
а
р
,
а
– коэффициенты гидромеханических потерь насоса, зависящих от угловой скорости, давления, и постоянная гидромеханических потерь;
u
д
– передаточное число редуктора между двигателем и насосом;
k
ут
– коэффициент объемных потерь насоса; для
Q
i
,
p
i
принимается знак «плюс», для
Q
j
,
p
j
– «минус».
Гидромотор. Математическая модель гидромотора содержит уравнение моментов в узле k , а также уравнения потоков на входе (узел i ) и выходе (узел j ) с учетом объемных потерь. Без учета неравномерности расхода (аналогично насосу) уравнения гидромотора имеют вид [1, 2]:
где
ω
k
– угловая скорость вала гидромотора;
q
м
– максимальный рабочий объем насоса;
f
(
q
)
– параметр регулирования; – 1
≤
f
(
q
)
≤
1;
М
н
– нагрузочный момент;
b
ω
,
b
р
,
b
– коэффициенты гидромеханических потерь гидромотора, зависящих от угловой скорости, давления, и постоянная гидромеханических потерь;
u
мех
– передаточное число редуктора рабочего механизма;
k
ут
– коэффициент объемных потерь насоса; для
Q
i
,
p
i
принимается знак «плюс», для
Q
j
,
p
j
– «минус».
Гидроцилиндр. Гидроцилиндр описывается уравнением баланса сил (сил давления, внешней нагрузки, сил трения) при поступательном движении поршня (узел k ) и уравнениями расходов на входе (узел i ) и выходе (узел j ). На основании общепринятого допущения об отсутствии утечек в гидроцилиндре с резиновыми и другими мягкими уплотнениями уравнения статики гидроцилиндра имеют вид [1, 2]:
где
v
k
– скорость перемещения поршня;
F
i
= π (
D
k i = π f ( D ц + D i ) H / 2, k j = π f ( D ц + D j ) H / 2. (5) Трубопровод. Математическая модель трубопровода с жидкостью состоит из равенства расходов на входе (узел i ) и выходе (узел j ) и уравнения потерь давления по длине и имеет вид [1, 2]:
где
здесь Re = 4 |
Q
i
| / (
Тупиковый участок трубопровода (полость). Для тупикового участка трубопровода потерями давления по длине можно пренебречь, и тогда уравнения статики тупикового участка трубопровода принимают вид:
Местное сопротивление (дроссель). Расход жидкости через дроссель связан с перепадом давления на входе (узел i ) и выходе (узел j ) известной зависимостью [1, 2]:
где
где
Клапаны.
где
F
i
и
F
j
– рабочие площади запорно-регулирующего элемента клапана со стороны напорной и сливной линии;
с
– жесткость пружины;
Клапан непрямого действия состоит из двух элементов: основного клапана с узлами r , s , t и вспомогательного клапана с узлами i , j , k . Если узел слива j является общим для обоих клапанов, то s = j . Математическая модель статики клапана непрямого действия имеет вид [2]:
где
Гидроаккумулятор. Для описания стационарного режима гидропневматического или пружинного аккумулятора необходимо записать уравнения равновесия поршня (мембраны) в узле k , уравнение расхода на входе (узел i ) и уравнение политропного процесса в газовой полости (узел j ) [1, 2]:
где
F
=
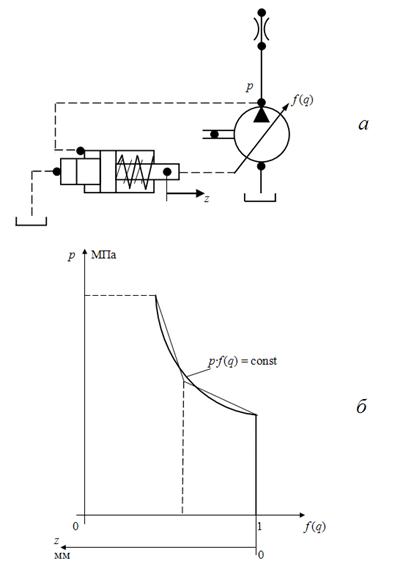
Регулятор мощности
предназначен для поддержания в определенном рабочем диапазоне насоса постоянства мощности, отбираемой от двигателя
pQ
= const. На самом деле, регулятор мощности обеспечивает постоянство величины:
p
f
(
q
)
= const. Однако, учитывая, что
Q
=
q
н
f
(
q
)
Тогда в статике регулятор мощности описывается следующим уравнением [1, 2]:
где
А
– коэффициент, учитывающий для аксиально-поршневых насосов дополнительный момент, действующий на качающий узел;
F
– рабочая площадь плунжера под давлением каждой из двух магистралей;
где
Колесо (колесный движитель). Для проведения тяговых расчетов гидрообъемных трансмиссий самоходных колесных машин необходимо рассмотреть в качестве одного из базовых элементов колесо (колесный движитель) – рис. 1. На схеме индексами i , j , k обозначены соответственно узлы входа (приводной вал колеса), выхода (точка контакта колеса с дорогой) и перемещения машины. Рассматриваемая здесь модель колесного движителя описывает жесткую связь колеса с гидромотором. С учетом принятых допущений математическая модель колеса (колесного движителя) в статике имеет вид:
где
М
i
– момент на колесе с учетом потерь в редукторе;
М
n
– момент, на валу гидромотора;
В установившемся режиме
окружная сила
R
на колесе связана с относительной пробуксовкой
где
Здесь
f
(|
δ
|) – функция буксования колеса (рис. 3);
ω
– угловая скорость колеса;
v
– скорость поступательного движения машины (узел
k
, рис. 1).
Величина радиуса колеса
r
зависит от статического прогиба колеса под нагрузкой
где
|
Содержание
>> Инженерная математика
>> Гидравлические системы
>> Статический расчет
>> Библиотека гидроэлементов и их математических моделей
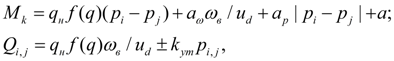 , (2)
, (2)
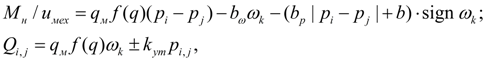 (3)
(3)
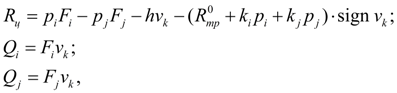 (4)
(4)
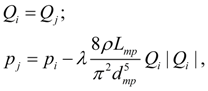 (6)
(6)
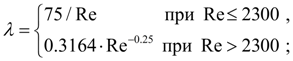 (7)
(7)
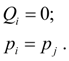 (8)
(8)
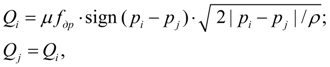 (9)
(9)
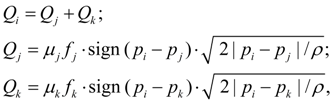 (10)
(10)
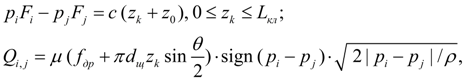 (11)
(11)
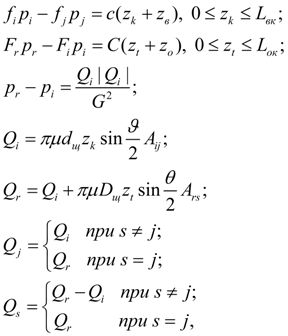 (12)
(12)
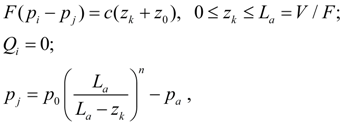 (14)
(14)
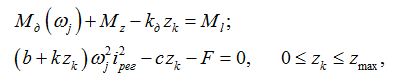 (16)
(16)
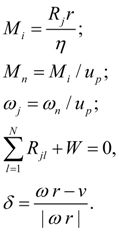 (17)
(17)
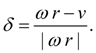 (19)
(19)