Интерполяция функций - Введение
Введение
Интерполяция
–операция приближения функции, заданной в отдельных точках внутри некоторого заданного промежутка. Простейшая задача интерполяции заключается в следующем. На отрезке
[
a
,
b
] заданы
n
+1 точек
 (
i
= 0, 1, 2, …,
n
) , называемые
узлами интерполяции
, и значения некоторой функции
(
i
= 0, 1, 2, …,
n
) , называемые
узлами интерполяции
, и значения некоторой функции
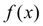 в этих точках
в этих точках
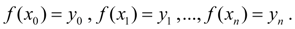 Требуется построить
интерполирующую
функцию
Требуется построить
интерполирующую
функцию
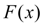 , принимающую в узлах интерполяции те же значения, что и
, принимающую в узлах интерполяции те же значения, что и
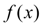 , т.е.
, т.е.
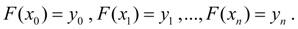 Геометрически это означает (рис. 1), что требуется найти некоторую кривую
Геометрически это означает (рис. 1), что требуется найти некоторую кривую
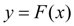 определенного типа, проходящую через заданный набор точек
определенного типа, проходящую через заданный набор точек
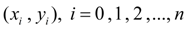 .
.
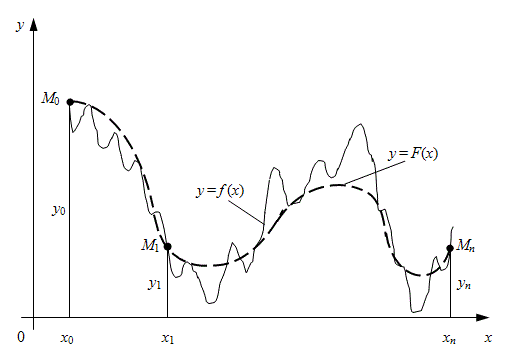
Рис. 1. Геометрическое представление интерполяции функции
В такой постановке задача интерполяции, вообще говоря, может иметь либо бесчисленное множество решений, либо совсем не иметь решений. Однако задача становится однозначно разрешимой, если вместо произвольной функции
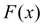 искать полином
искать полином
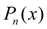 степени не выше
n
, удовлетворяющий условиям:
степени не выше
n
, удовлетворяющий условиям:
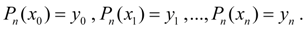 (1)
(1)
Полученную интерполяционную формулу
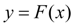 используют для приближенного вычисления значений данной функции
используют для приближенного вычисления значений данной функции
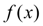 для тех
х
, которые отличны от узлов интерполяции. Такая операция называется
интерполяцией
функции
для тех
х
, которые отличны от узлов интерполяции. Такая операция называется
интерполяцией
функции
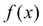 .
.
|
