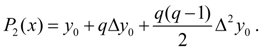Первая интерполяционная формула Ньютона
Пусть в равноотстоящих точках
Условия (1) эквивалентны равенствам:
при
Опуская выкладки, приведенные в [1] , окончательно получим первую интерполяционную формулу Ньютона :
где
В частных случаях имеем: при n = 1 – формулу линейной интерполяции :
при n = 2 – формулу квадратичной или параболической интерполяции :
|
Содержание
>> Прикладная математика
>> Численные методы
>> Интерполяция функций
>> Первая интерполяционная формула Ньютона
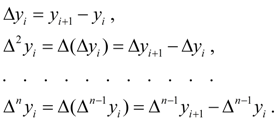 (2)
(2)
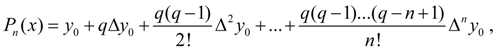 (3)
(3)
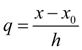 – число шагов интерполяции от начальной точки
– число шагов интерполяции от начальной точки