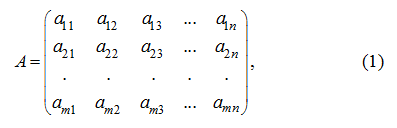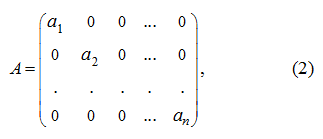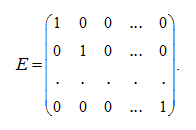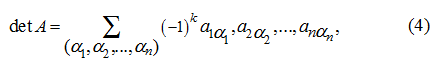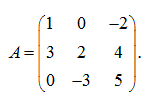Основные определения

Система из mn чисел (действительных, комплексных), или функций, или других объектов, записанная в виде прямоугольной таблицы, состоящей  из m строк и n столбцов:

называется матрицей.

Числа (функции, другие объекты) , составляющие матрицу (1), называются элементами матрицы . Здесь первый индекс i обозначает номер строки, а второй j – номер столбца, на пересечении которых расположен данный элемент матрицы.

Для матрицы (1) существует сокращенная запись:

или просто . В этом случае говорят, что матрица А имеет размерность m × n . Если m = n , то матрица называется квадратной порядка n . Если то матрица называется прямоугольной . Матрица размерности 1 × n называется вектором-строкой , а матрица размерности m × 1– вектором-столбцом . Обычное число (скаляр) можно считать матрицей размерности 1 × 1.

Если квадратная матрица имеет вид:

то она называется диагональной .

Если в диагональной матрице (2) все диагональные элементы равны 1, то матрица называется единичной и обозначается:

Используя символ Кронекера:

можно записать

Матрица, у которой все элементы равны 0, называется нулевой и обозначается 0.

Элементы квадратной матрицы n -го порядка образуют так называемую главную диагональ матрицы.Сумма элементов главной диагонали называется c ледом (Trace, Spur) матрицы:

С квадратной числовой матрицей связано понятие определитель (детерминант) :

Матрица и ее определитель разные (хотя и связанные) понятия. Числовая матрица А – это упорядоченная система чисел, записанная в виде прямоугольной таблицы, а ее определитель  det A – это число, равное:

где сумма (4) распространяется на возможные перестановки элементов 1, 2, ... , n и, следовательно, содержит n ! слагаемых, причем k = 0, если перестановка четная и k = 1, если перестановка нечетная.

П р и м е р .  Вычислить определитель матрицы

Р е ш е н и е .  Согласно (3) имеем: