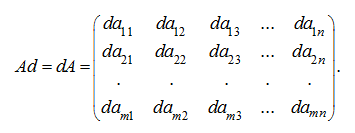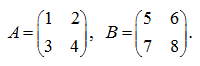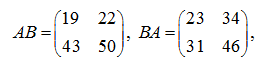Операции над матрицами

1. Равенство матриц

Две матрицы одной и той же размерности считаются равными: А = В ,  если равны их соответствующие элементы, то есть

2. Сумма и разность матриц

Суммой двух матриц одной и той же размерности называется матрица той же размерности, элементы которой равны сумме соответствующих элементов матриц А и В , то есть
Из определения суммы матриц непосредственно следуют ее основные свойства:
1) А+В = В+А ;
2) А+( В+С ) = ( А+В )+С ;
3) А+ 0 = А .
Аналогичным образом определяется разность матриц А – В .

3. Умножение матрицы на число

Произведением матрицы на число d (или произведением числа d на матрицу  А ) называется матрица , элементы которой являются произведениями элементов матрицы А на число d . Иными словами,

Из определения произведения числа на матрицу непосредственно следуют его основные свойства:
1)  1 А = А 1= А ;
2)  0 А = А 0=0 ;
3) d ( hA ) = ( dh ) A = h ( dA ) ;
4)  ( d+h ) A=dA+hA ;
5) d ( A+B ) = dA+dB .
Здесь А и В – матрицы, d и h – числа.

Заметим, что для квадратной матрицы А порядка n имеет место равенство:

Матрица – А= (–1) А называется противоположной . Очевидно, что для двух матриц А и В одинаковой размерности имеет место равенство: А – В = А + ( – В ) .

4. Умножение матриц

Пусть  размерности матриц А и В равны соответственно m × n и n × k , то есть число столбцов матрицы А равно числу строк матрицы В , тогда для этих двух матриц определена матрица С размерности m × k , являющаяся их произведением: С = АВ . Элементы матрицы С вычисляются по формуле:

Отсюда следует, что элемент, стоящий в i -ой строке и j -ом столбце матрицы-произведения, равен сумме произведений элементов i -ой строки первой матрицы на соответствующие элементы j -ого столбца второй матрицы.

Из определения произведения матриц следует, что можно умножать квадратные матрицы только одного и того же порядка.

Основные свойства матричного произведения:
1) А ( ВС ) = ( АВ ) С ;
2) d ( АВ ) = ( dA ) B ;
3)  ( А+В ) С= АС+ ВС ;
4) С ( А+В ) = СА+ СВ .
Здесь А , В и С – матрицы, d – число.

Произведение двух матриц в общем случае не коммутативно, то есть АВ ≠ ВА .
В частном случае, когда АВ = ВА , матрицы А и В называются коммутативными (перестановочными). Как легко убедиться, единичная матрица Е перестановочна с любой квадратной матрицей того же порядка, причем АЕ = ЕА = А . Следовательно, при умножении матриц единичная матрица Е играет ту же роль, что единица при умножении чисел.

Для квадратных матриц А и В одного и того же порядка имеет место равенство: det ( AB ) = det ( BA ) = det A · det B .

П р и м е р  1.  Даны матрицы

Вычислить определители левого и правого произведений АВ и ВА .

Р е ш е н и е .

или окончательно:

то есть АВ ≠ ВА .

Однако, определители произведений АВ и ВА равны: