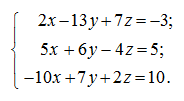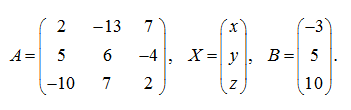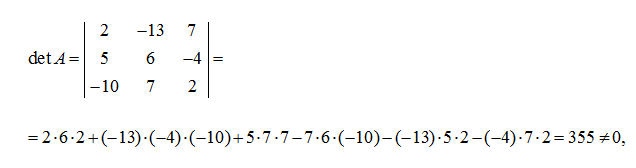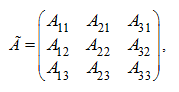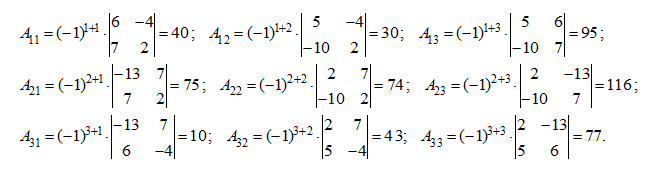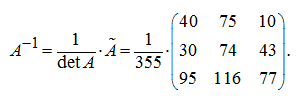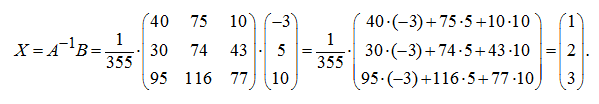Пример

Решить систему линейных уравнений, используя матричный аппарат:

Р е ш е н и е

Запишем данную систему линейных уравнений в матричной форме:

где

Решение данной системы линейных уравнений в матричной форме имеет вид:

где – матрица, обратная к матрице А .
Определитель матрицы коэффициентов А равен:

следовательно, матрица А имеет обратную матрицу .

Сначала найдем присоединенную матрицу Ã , которая в данном примере имеет вид:

где – алгебраические дополнения соответствующих элементов матрицы А .
В нашем случае получим:

Таким образом,

Тогда обратная матрица равна:

Теперь найдем решение заданной системы уравнений. Так как, то

Таким образом, решение данной системы уравнений: