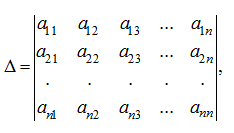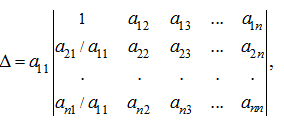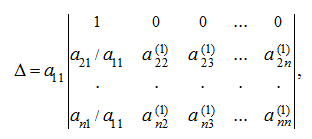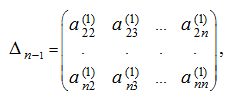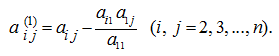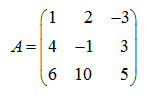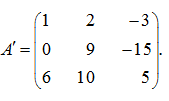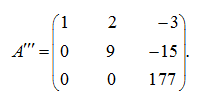Элементарные преобразования матриц

Элементарные преобразования матрицы находят широкое применение в различных математических задачах. Например, они составляют основу известного метода Гаусса (метода исключения неизвестных) для решения системы линейных уравнений [1].

К элементарным преобразованиям относятся:
1)  перестановка двух строк (столбцов);
2)  умножение всех элементов строки (столбца) матрицы на некоторое число, не равное нулю;
3)  сложение двух строк (столбцов) матрицы, умноженных на одно и то же число, отличное от нуля.

Две матрицы называются эквивалентными , если одна из них может быть получена из другой после конечного числа элементарных преобразований. В общем случае эквивалентные матрицы равными не являются, но имеют один и тот же ранг.

Вычисление определителей с помощью элементарных преобразований

С помощью элементарных преобразований легко вычислить определитель матрицы. Например, требуется вычислить определитель матрицы:

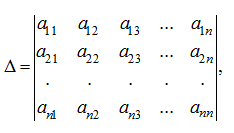
где 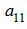≠ 0.
Тогда можно вынести множитель :

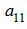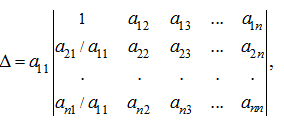
теперь, вычитая из элементов j - го столбца 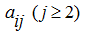соответствующие элементы первого столбца, умноженные на 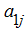, получим определитель:

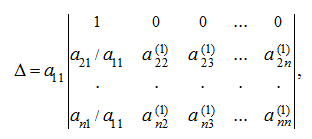
который равен: 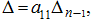где

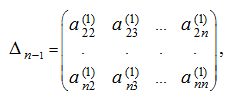
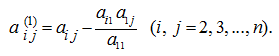
Затем повторяем те же действия для 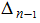и, если все элементы 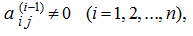то тогда окончательно получим:

Если для какого-нибудь промежуточного определителя 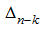окажется, что его левый верхний элемент 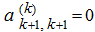, то необходимо переставить строки или столбцы в 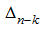так, чтобы новый левый верхний элемент был не равен нулю. Если Δ ≠ 0, то это всегда можно сделать. При этом следует учитывать, что знак определителя меняется в зависимости от того, какой элемент 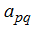является главным (то есть, когда матрица преобразована так, что 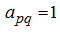). Тогда знак соответствующего определителя равен .

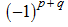П р и м е р . С помощью элементарных преобразований привести матрицу

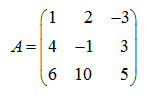
к треугольному виду.

Р е ш е н и е . Сначала умножим первую строку матрицы на 4, а вторую на (–1) и прибавим первую строку ко второй:

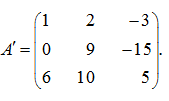
Теперь умножим первую строку на 6, а третью на (–1) и прибавим первую строку к третьей:

Наконец, умножим вторую строку на 2, а третью на (–9) и прибавим вторую строку к третьей:

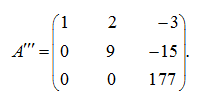
В результате получена верхняя треугольная матрица