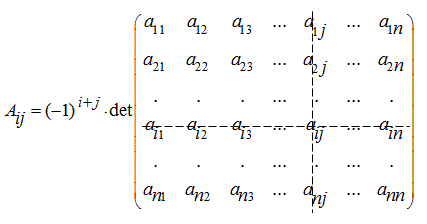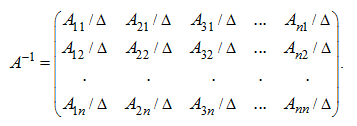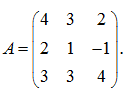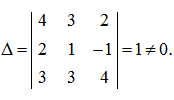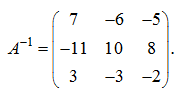|
Матричная алгебра - Обратная матрица
Обратная матрица
Обратной матрицей
называется матрица, которая при умножении как справа, так и слева на данную матрицу дает единичную матрицу.
Обозначим обратную матрицу к матрице
А
через
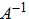 , тогда согласно определению получим:
, тогда согласно определению получим:
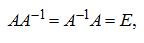
где
Е
– единичная матрица.
Квадратная матрица
называется
неособенной
(
невырожденной
), если ее определитель не равен нулю. В противном случае она называется
особенной
(
вырожденной
) или
сингулярной
.
Имеет место теорема:
всякая неособенная матрица имеет обратную матрицу.
Операция нахождения обратной матрицы называется
обращением
матрицы. Рассмотрим алгоритм обращения матрицы. Пусть дана неособенная матрица
n
-го порядка:

где Δ = det
A
≠ 0.
Алгебраическим дополнением элемента
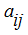 матрицы
n
-го порядка
А
называется взятый с определенным знаком определитель матрицы (
n
–1)-го порядка, полученной вычеркиванием
i
-ой строки и
j
-го столбца матрицы
А
:
матрицы
n
-го порядка
А
называется взятый с определенным знаком определитель матрицы (
n
–1)-го порядка, полученной вычеркиванием
i
-ой строки и
j
-го столбца матрицы
А
:
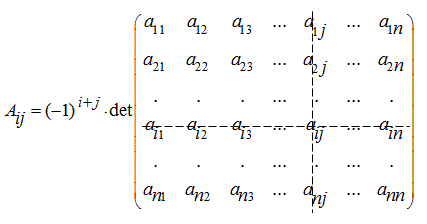
Составим так называемую
присоединенную
матрицу:

где
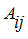 – алгебраические дополнения соответствующих элементов
– алгебраические дополнения соответствующих элементов
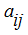 матрицы
А
.
матрицы
А
.
Заметим, что алгебраические дополнения элементов строк матрицы
А
размещаются в соответствующих столбцах матрицы
Ã
, то есть одновременно производится транспонирование матрицы.
Разделив все элементы матрицы
Ã
на Δ – величину определителя матрицы
А
, получим в результате обратную матрицу
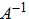 :
:
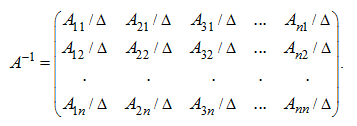
Отметим ряд особых свойств обратной матрицы:
1) для данной матрицы
А
ее обратная матрица
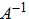 является единственной;
является единственной;
2) если существует обратная матрица
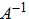 , то
правая обратная
и
левая обратная
матрицы совпадают с ней;
, то
правая обратная
и
левая обратная
матрицы совпадают с ней;
3) особенная (вырожденная) квадратная матрица не имеет обратной матрицы.
Основные свойства обратной матрицы:
1) определитель обратной матрицы и определитель исходной матрицы являются обратными величинами;
2) обратная матрица произведения квадратных матриц равна произведениюобратных матриц сомножителей, взятому в обратном порядке:
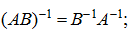
3) транспонированная обратная матрица равна обратной матрице от данной транспонированной матрицы:
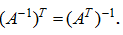
П р и м е р . Вычислить матрицу, обратную данной:
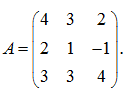
Р е ш е н и е . Определитель матрицы
А
равен:
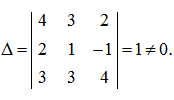
Следовательно, матрица
А
неособенная. Присоединенная матрица
Ã
имеет вид:

Разделив все элементы присоединенной матрицы
Ã
на Δ = 1, получим обратную матрицу
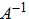 :
:
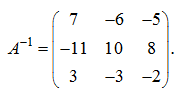
Проверим, что действительно,
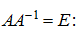

Таким образом, найденная матрица
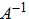 является обратной для заданной матрицы
А
.
является обратной для заданной матрицы
А
.
|