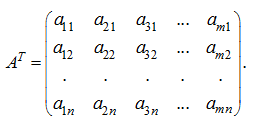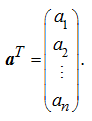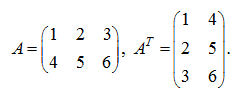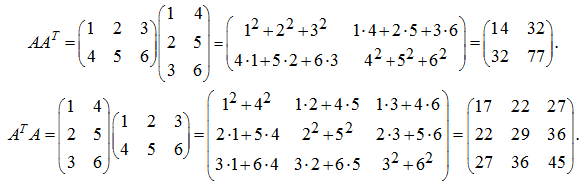Транспонированная матрица

Замена в матрице размерности m × n

строк соответственно столбцами, дает так называемую транспонированную матрицу размерности n × m :

В частности, для вектора-строки транспонированной матрицей является вектор-столбец

Основные свойства транспонированной матрицы:
1) дважды транспонированная матрица совпадает с исходной:

2) транспонированная матрица суммы матриц равна сумме транспонированных матриц слагаемых, то есть

3) транспонированная матрица произведения матриц равна произведению транспонированных матриц сомножителей, взятому в обратном порядке:

Для квадратной матрицы имеет место очевидное равенство:

Если матрица совпадает со своей транспонированной

то она называется симметрической . Из последнего равенства следует, что симметрическая матрица является квадратной, и ее элементы, симметричные относительно главной диагонали, равны между собой:
Очевидно, что произведение является симметрической матрицей, так как, используя свойство 3, получим:

П р и м е р .  Даны матрица А и транспонированная матрица :

Вычислить произведения

Р е ш е н и е .

Как и следовало ожидать, получены симметрические матрицы.