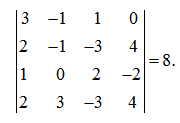Ранг матрицы

Рассмотрим прямоугольную матрицу:

Если выбрать в этой матрице произвольным образом k строк и k столбцов, где k ≤ min ( m , n ), то элементы, стоящие на пересечении этих строк и столбцов, образуют квадратную матрицу порядка k . Определитель этой субматрицы называется минором k -го порядка матрицы А .

Ранг матрицы – это максимальный порядок не равного нулю минора матрицы.

Иными словами, ранг матрицы А равен r , если:
1) существует хотя бы один минор r -го порядка матрицы А , не равный нулю;
2) все миноры порядка r +1 и выше равны нулю или не существуют.

Ранг нулевой матрицы (матрицы, состоящей из нулей) считается равным нулю.

Разность  min ( m , n ) – r называется дефектом матрицы . Если дефект матрицы равен нулю, то матрица имеет максимально возможный ранг.

П р и м е р .  Определить ранг матрицы

Р е ш е н и е .  Левый минор четвертого порядка данной матрицы равен

Следовательно, ранг матрицы равен 4.