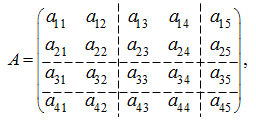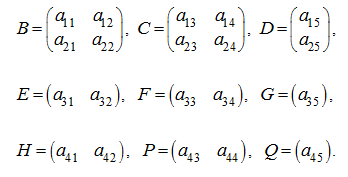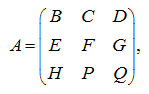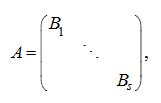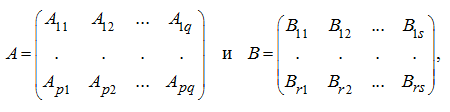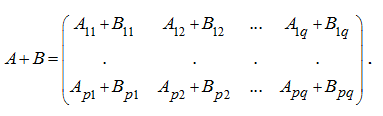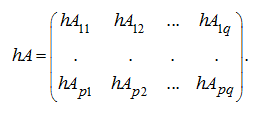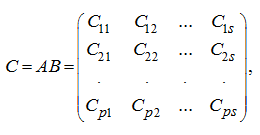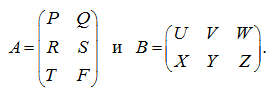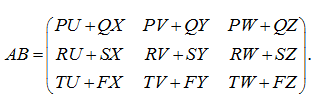Клеточные матрицы

Рассмотрим некоторую матрицу А и разобьем ее на матрицы более низкого порядка:

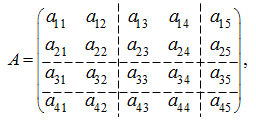
которые  называются клетками или блоками .

Здесь клетками (блоками) являются матрицы:

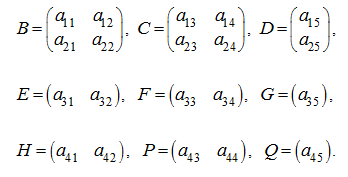
Теперь матрицу А можно рассматривать как клеточную или блочную :

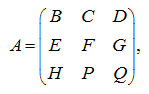
элементами которой являются клетки (блоки).

Очевидно, что разбиение произвольной матрицы на клетки (блоки) может быть выполнено различными способами. В частном случае клеточная матрица может оказаться квазидиагональной :

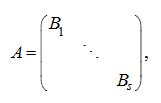
где клетки 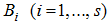– квадратные матрицы (вообще говоря, разных порядков), а вне клеток стоят нули.
Отметим, что
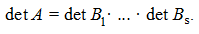
Клеточные матрицы одной и той же размерности и с одинаковым разбиением называются конформными .

Действия над клеточными матрицами осуществляются по тем же правилам, что и над обычными матрицами.

1. Сложение и вычитание клеточных матриц

Пусть имеются две конформные клеточные матрицы:

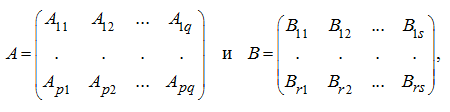
где p = r , q = s и клетки 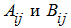одинаковой размерности. Тогда

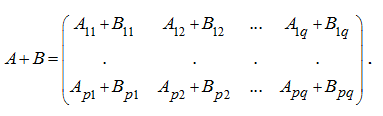
Аналогично выполняется вычитание клеточных матриц.

2. Умножение клеточных матриц

Умножение клеточной матрицы на число (скаляр)

Пусть А – клеточная матрица и h – число, тогда имеем:

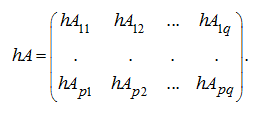
Умножение клеточных матриц

Рассмотрим две конформные клеточные матрицы:

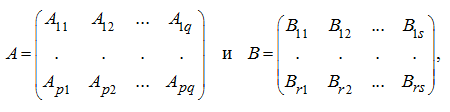
причем q = r .

Пусть все клетки 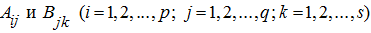такие, что число столбцов клетки 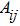равно числу строк клетки 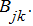(Например, очевидно, что это имеет место в частном случае, когда все клетки 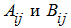– квадратные  матрицы и имеют одинаковый порядок). Тогда легко показать, что произведение матриц А и В – тоже клеточная матрица:

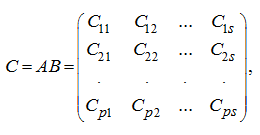
где 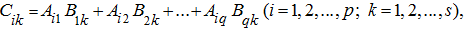то есть умножение клеточных матриц аналогично умножению числовых [2].

П р и м е р . Перемножить клеточные матрицы

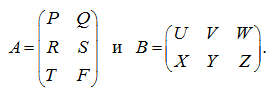
Р е ш е н и е .
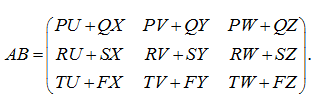