Численное дифференцирование - Введение
Введение
При решении инженерно-технических и других прикладных задач часто бывает необходимо найти производную определенного порядка от функции
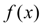 , заданной таблично. Кроме того, иногда в силу сложности аналитического выражения функции
, заданной таблично. Кроме того, иногда в силу сложности аналитического выражения функции
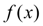 ее непосредственное дифференцирование слишком затруднительно. В этих случаях обычно используют
численное дифференцирование
. Здесь существует множество различных приемов и способов [1– 3]. Одной из самых простых формул для
вычисления производной
функции
ее непосредственное дифференцирование слишком затруднительно. В этих случаях обычно используют
численное дифференцирование
. Здесь существует множество различных приемов и способов [1– 3]. Одной из самых простых формул для
вычисления производной
функции
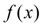 является формула вычисления производной
через равноотстоящие узлы
[2, 3]:
является формула вычисления производной
через равноотстоящие узлы
[2, 3]:
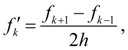 (1)
(1)
где
h
– шаг,
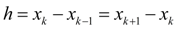 ,
,
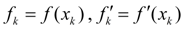 .
.
Иногда заданную функцию
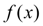 на интересующем нас отрезке [
a
,
b
] заменяют интерполирующей функцией
на интересующем нас отрезке [
a
,
b
] заменяют интерполирующей функцией
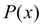 , чаще всего полиномом, а затем полагают [1]:
, чаще всего полиномом, а затем полагают [1]:
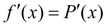 , (2)
, (2)
при
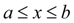 .
.
Аналогичным образом вычисляют производные функции
 высших порядков.
высших порядков.
Если известна погрешность интерполирующей функции
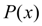 :
:
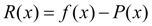 , (3)
, (3)
то погрешность производной
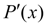 равна:
равна:
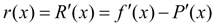 , (4)
, (4)
т.е.
погрешность производной интерполирующей функции равна производной от погрешности этой функции
. Это справедливо и для производных высших порядков. Вообще говоря, численное дифференцирование является операцией менее точной, чем интерполирование функции, иными словами близость друг к другу ординат функций
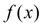 и
и
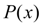 на отрезке [
a
,
b
] еще не гарантирует близости на этом отрезке их производных, т.е. малого расхождения угловых коэффициентов касательных к рассматриваемым кривым при одних и тех же значениях аргумента (рис.1).
на отрезке [
a
,
b
] еще не гарантирует близости на этом отрезке их производных, т.е. малого расхождения угловых коэффициентов касательных к рассматриваемым кривым при одних и тех же значениях аргумента (рис.1).
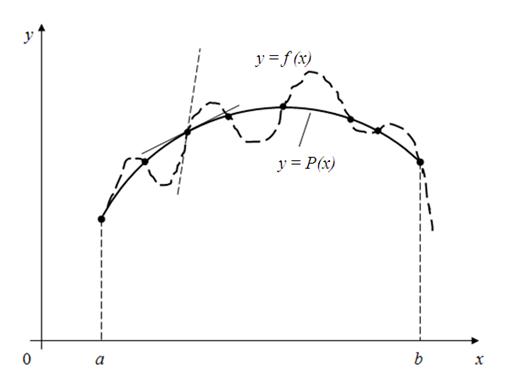
Рис.1. Разница в производных заданной функции
y
=
f
(
x
)
и интерполирующей функции
y
=
P
(
x
)
|
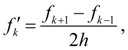 (1)
(1)
