Формулы численного дифференцирования
1. На основе первой инерполяционной формулы Ньютона
Для нахождения первой и второй производных функции
Раскрывая скобки и учитывая, что
получим:
Аналогично, учитывая
получим:
Таким же образом можно при необходимости вычислить производную функции
2. На основе инерполяционной формулы Стирлинга
Пусть
где для краткости записи введены следующие обозначения:
и т.д.
Из (8) с учетом того, что
|
Содержание
>> Прикладная математика
>> Численные методы
>> Численное дифференцирование
>> Формулы численного дифференцирования
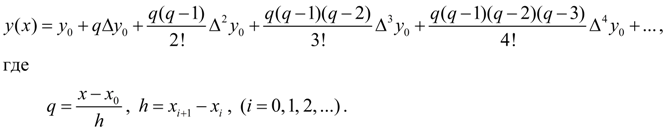 (5)
(5)
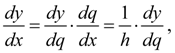
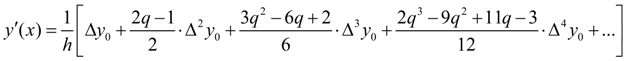 . (6)
. (6)
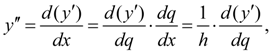
 . (7)
. (7)
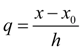 и заменяя функцию
и заменяя функцию
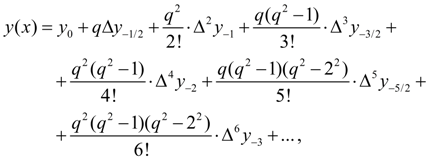 (8)
(8)
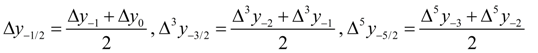
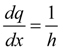 , следует:
, следует:
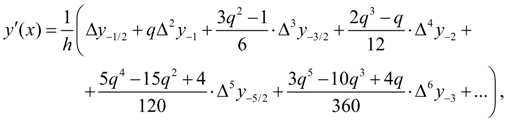 (9)
(9)
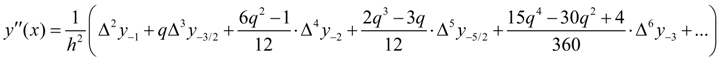 . (10)
. (10)