Введение
В инженерной практике постоянно возникает необходимость вычисления определенных интегралов. Если некоторая функция
где
Однако в большинстве случаев не существует конечных формул, выражающих неопределенный интеграл в виде комбинации элементарных функций, так как найти первообразную
Численное интегрирование – это область приближенных методов вычисления определенных интегралов. Существует множество методов численного интегрирования: формулы трапеций, Симпсона, Гаусса, Ньютона-Котеса, Чебышева и др. Мы ограничимся здесь рассмотрением двух наиболее простых и широко применяемых алгоритмов: правила трапеций и метода Симпсона. Итак, пусть требуется вычислить определенный интеграл:
где
Задача численного интегрирования заключается в вычислении значения интеграла (2) по ряду значений подынтегральной функции
|
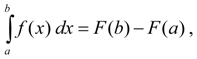 (1)
(1)
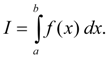 (2)
(2)