Формула трапеций
Рассмотрим интеграл (2), представляющий собой,
как известно
, площадь под кривой
Разобьем теперь интервал интегрирования (
a
,
b
) на
n
равных частей длиной
Рассмотрим один из этих интервалов (рис. 2).
Площадь под кривой
Предположим, что шаг интегрирования
h
достаточно мал, тогда эту площадь без существенной погрешности можно приравнять к площади трапеции
ABCD
. Так как
где
Подставляя (3) в (4), окончательно получим [3, 4]:
Это и есть формула трапеций . Правило трапеций – один из простейших методов численного интегрирования, и хотя погрешности вычислений этим способом больше, чем в других методах, он пользуется большим спросом благодаря своей наглядности и простоте. |
Содержание
>> Прикладная математика
>> Численные методы
>> Численное интегрирование
>> Формула трапеций
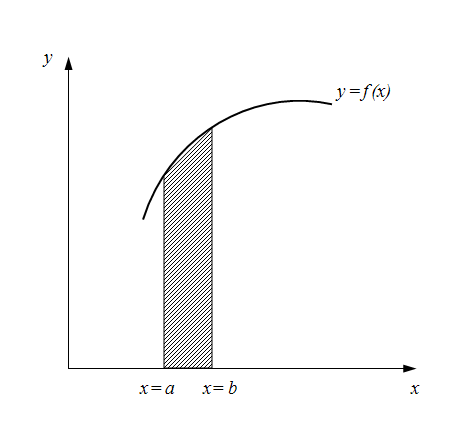
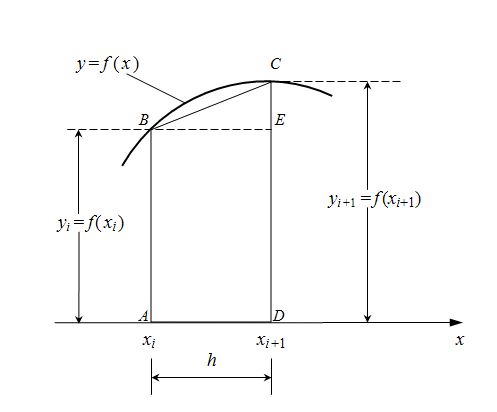
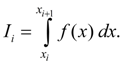
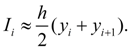 (3)
(3)
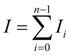 , (4)
, (4)
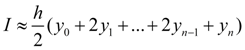 . (5)
. (5)