Выравнивание статистических распределений. Кривые ПирсонаДля выравнивания (аппроксимации) статистических распределений используется множество различных методов: полиномиальной аппроксимации, рядами Шарлье, пертурбационными многочленами Крамера, метод Пирсона и др. Основным недостатком полиномиальной аппроксимации является формальность получаемых распределений – тип аппроксимации не связан с природой случайного явления. Методы Шарлье и Крамера подходят к аппроксимации распределений, приближенных к нормальному. В отличие от них метод Пирсона достаточно универсален и охватывает практически все известные виды статистических распределений. Пирсон [1, 2] предложил для описания статистического распределения случайной величины Х использовать решения дифференциального уравнения:
где началом отсчета х служит его среднее значение, М – мода. Коэффициенты в уравнении (1) могут быть вычислены с помощью центральных моментов .
При введении обозначений
Введем вспомогательную величину:
Тогда систему уравнений (2) можно переписать в виде:
Вычислим дискриминант знаменателя в уравнении (1):
Обозначим
Тогда
Общий интеграл уравнения (1) существенно зависит от вида корней квадратного уравнения
1. При
2. При
3. При
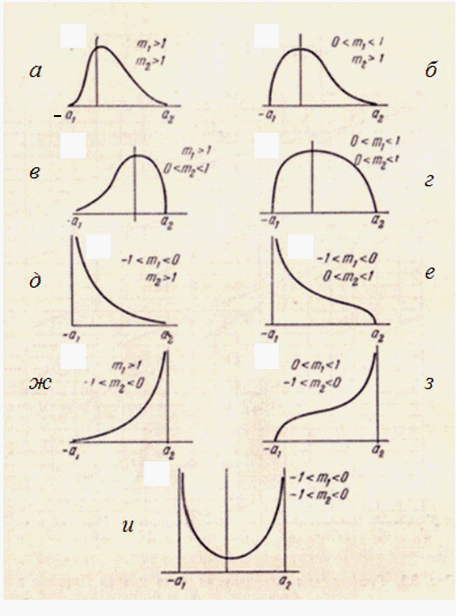
Каждому из этих случаев соответствует один из основных типов кривых Пирсона –
I
,
IV
и
VI
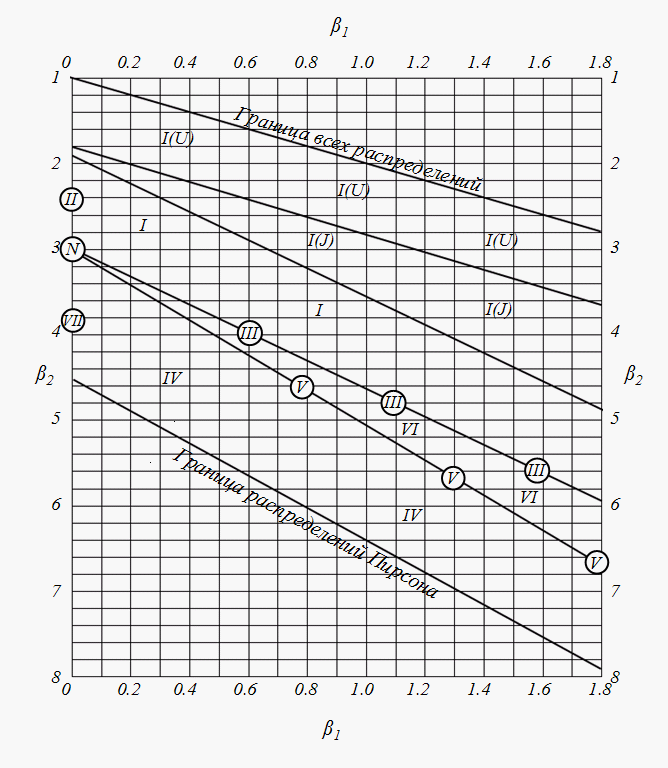
. Остальные девять типов и кривая нормального распределения – их частные или граничные случаи. Чаще всего на практике встречаются первые семь типов кривых Пирсона. На рис.1 приведен график для определения типа кривой по параметрам
Рассмотрим уравнения кривых Пирсона
I
–
VII
типов и способы определения входящих в них параметров [1, 2].
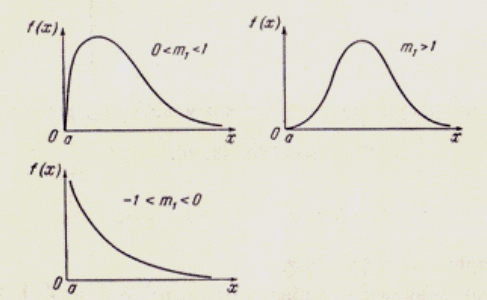
Кривая I типа соответствует κ < 0; ее уравнение имеет вид:
Показатели степени
причем при
Коэффициенты
где
Здесь Г(z) – гамма-функция :
Областью определения кривой
I
типа является интервал:
В зависимости от значений
1. При
2. При разных знаках
3. При
Кривая
IV
типа
соответствует
где
Знак
ν
выбирается противоположным знаку
а
Начало координат берется в точке
Кривая VI типа соответствует κ > 1 и описывается уравнением:
Здесь
Начало координат берется в точке
Кривая лежит на интервале от
а
до +∞ при
Следующая группа кривых Пирсона соответствует частным значениям критерия
κ
.
Кривая
III
типа
имеет место при
Мода
Частным случаем кривой Пирсона
III
типа при
Начало координат – в точке
Здесь
Функция
y
=
f
(
x
) определена при всех
х
> 0. Начало координат – в точке
Рис. 5. Кривая Пирсона V типа
При
κ
= 0 в зависимости от значения
где
Кривая
VII
типа
соответствует
где
Коэффициент
|
Содержание
>> Прикладная математика
>> Математическая статистика
>> Обработка результатов эксперимента
>> Выравнивание статистических распределений. Кривые Пирсона
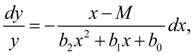 (1)
(1)
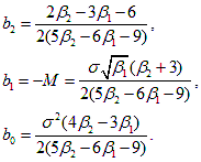 (2)
(2)
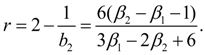 (3)
(3)
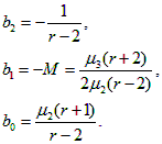 (2
а
)
(2
а
)
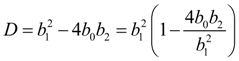 .
.
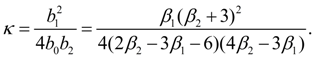 (4)
(4)
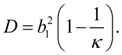
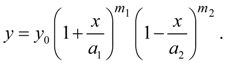 (5)
(5)
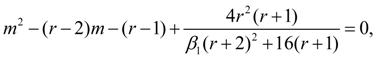 (6)
(6)

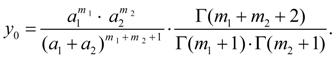 (8)
(8)
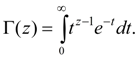 (9)
(9)
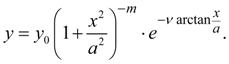 (10)
(10)
 (11)
(11)
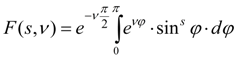 – табулированная функция.
– табулированная функция.
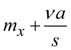 (здесь
(здесь
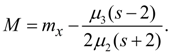
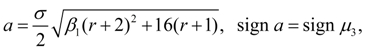 (14)
(14)
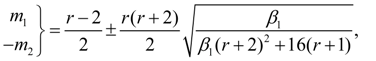 (15)
(15)
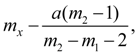 а начальная ордината
а начальная ордината
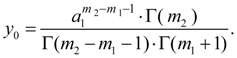 (16)
(16)
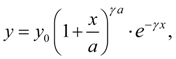 (17)
(17)
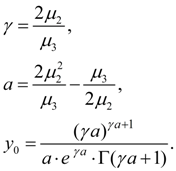 (18)
(18)
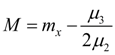 существует при
существует при
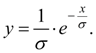 (19)
(19)
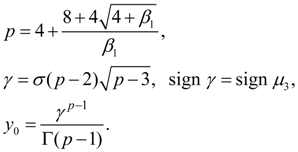 (21)
(21)
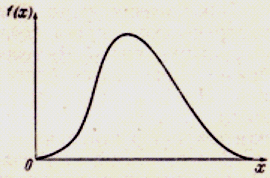
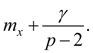 Общий вид кривой представлен на рис. 5.
Общий вид кривой представлен на рис. 5.
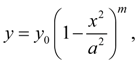 (22)
(22)
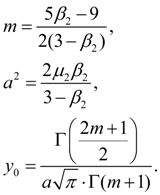 (23)
(23)
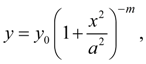 (24)
(24)
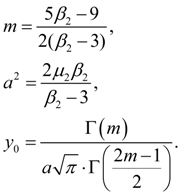 (25)
(25)
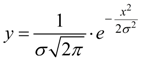 (26)
(26)