Метод характеристикМетод характеристик – это метод численного интегрирования систем дифференциальных уравнений в частных производных гиперболического типа. Впервые для ряда частных случаев был рассмотрен в работах Даламбера. В настоящее время метод характеристик широко применяется в задачах распространения волн в гидрогазодинамике. Так, динамика потока жидкости с учетом распределенных параметров по длине трубопровода (давления, скорости потока, массы, вязкого трения) описывается системой квазилинейных гиперболических уравнений в частных производных [4–6]:
где
p
,
u
– средние по сечению давление и скорость потока жидкости;
t
– время;
х
– координата по длине трубы;
ρ
- плотность жидкости;
Интегрирование нелинейных уравнений (18) проведем численным методом характеристик , в соответствии с которым исходные дифференциальные уравнения в частных производных (18) заменяются обыкновенными дифференциальными уравнениями
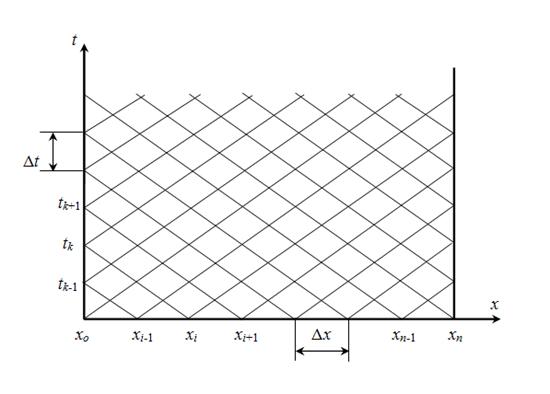
cправедливыми вдоль прямых и обратных характеристик dx = ± c dt . Численное интегрирование уравнений (19) методом характеристик осуществляется следующим образом. На плоскости xt (рис.4) строится сетка прямых и обратных характеристик, причем шаг интегрирования по длине Δ x связан с шагом интегрирования по времени Δ t линейным соотношением: Δ x = c Δ t . После перехода в уравнениях (19) к конечным разностям с учетом заданных граничных условий решаем полученную систему уравнений методом итераций.
Рассмотрим решение задачи (18) – (19) методом характеристик при определенных граничных условиях. Введем в узлах сетки характеристик (рис.4) следующие обозначения: p ( x i , t k ) = p ik ; u ( x i , t k ) = u ik ; λ ( x i , t k ) = λ ik . Тогда с учетом граничных условий u ok = f ( t k ), u nk = g ( t k ) после замены в уравнениях (19) производных конечно-разностными отношениями, а переменных p, u и λ – их средними значениями в соседних узлах сетки на прямой и обратной характеристиках [соответственно ( x i , t k ) , ( x i – 1 , t k – 1 ) и ( x i , t k ) , ( x i + 1 , t k – 1 )], получим следующую систему нелинейных алгебраических уравнений:
где f ( t k ) и g ( t k ) – функции времени в граничных узлах трубопровода, определяющие внешние возмущения, действующие на поток жидкости (например, пульсация расхода из-за кинематики насоса, объемное или дроссельное регулирование и т.д.); λ ik – коэффициент гидравлического сопротивления в узле ( x i , t k ):
где
Полученная система уравнений (20) – (21) решается итерационным методом. |
Содержание
>> Прикладная математика
>> Численные методы
>> Уравнения математической физики
>> Метод характеристик
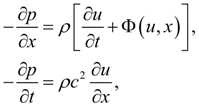 (18)
(18)
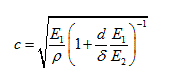 – скорость звука в жидкости с учетом упругости стенок трубопровода,
Е
1
– объемный модуль упругости жидкости;
Е
2
– модуль упругости материала
трубы;
d, δ
– внутренний диаметр и толщина стенки трубопровода; Φ (
u
,
x
) – нелинейная функция вязкого трения. Для
трубопровода круглого сечения
– скорость звука в жидкости с учетом упругости стенок трубопровода,
Е
1
– объемный модуль упругости жидкости;
Е
2
– модуль упругости материала
трубы;
d, δ
– внутренний диаметр и толщина стенки трубопровода; Φ (
u
,
x
) – нелинейная функция вязкого трения. Для
трубопровода круглого сечения
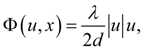 где
λ
– коэффициент гидравлического сопротивления, зависящий от числа Рейнольдса Re =
u d / ν
, здесь
ν
– кинематическая вязкость жидкости.
где
λ
– коэффициент гидравлического сопротивления, зависящий от числа Рейнольдса Re =
u d / ν
, здесь
ν
– кинематическая вязкость жидкости.
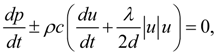 (19)
(19)
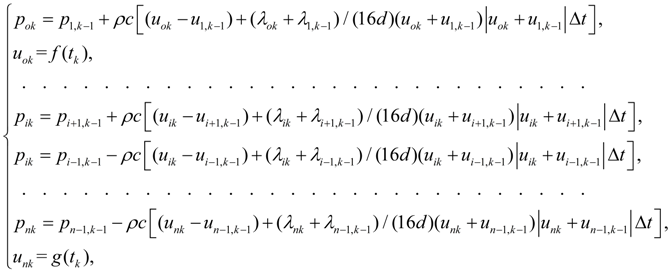 (20)
(20)
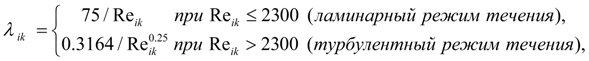 (21)
(21)