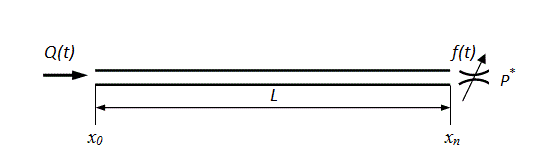
Пример: решение гиперболического уравненияДинамика давлений в трубопроводе с жидкостью Рассмотрим динамические процессы в трубопроводе с жидкостью с объемным регулированием (переменным расходом) Q ( t ) на входе и дроссельным регулированием f ( t ) на выходе (рис.5).
Рис. 5. Расчетная схема трубопровода с жидкостью После перехода в уравнениях (19) к конечным разностям зададим в точке х 0 следующие граничные условия для скорости потока u ok : при линейном изменении расхода 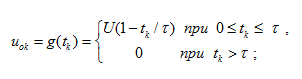 (22)
(22)
при пульсации расхода Граничные условия для скорости u nk в точке х n имеют вид: 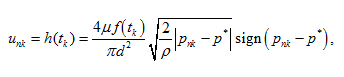 (24)
(24)
где μ – коэффициент расхода; f ( t ) – переменная площадь проходного сечения дросселя (рис.5), аналогичная зависимости (22); р* – постоянное давление подпора за дросселем. Проведем численный анализ динамики жидкости в трубопроводе при внешних возмущенях (22) – (24).
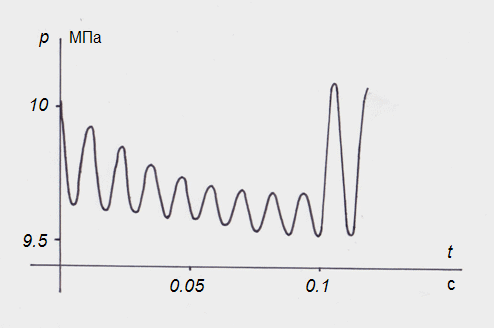
Рис. 6. Динамика давления на входе в трубопровод при объемном регулировании по линейному закону На рис.6 представлен график изменения во времени давлений на входе в трубопровод длиной L = 3 м при изменении расхода жидкости на входе по линейному закону (22), характерному для объемного регулирования (например, подачи насоса). При изменении расхода от максимального U до нуля за время τ = 0.1 сек. имеют место колебания давления на первой резонансной частоте с / 4 L (в данном случае ~ 85 Гц). При прекращении подачи жидкости в момент времени t = 0.1 сек. амплитуда колебаний давления резко возрастает из-за скачка инерционного напора du ok / dt .
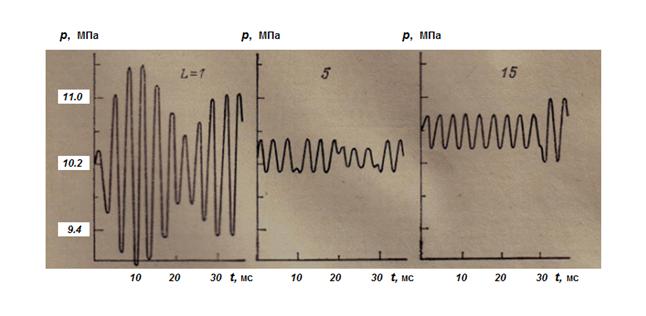
На рис.7 представлены динамические процессы давлений на входе трубопроводов длиной
L
= 1, 5 и 15 м при пульсирующем расходе жидкости
Q ( t )
.
τ < 2L / c . (25) Условие (25) рассматривалось как критерий при определении диапазона изменения параметров, численные значения которых для различных вариантов расчета приведены в таблице.
Здесь L – длина трубопровода; Е 1 – объемный модуль упругости рабочей жидкости; Е 2 – модуль упругости материала стенки трубы; f – минимальная площадь проходного сечения дросселя; τ – время перекрытия дросселя. Фиксированные величины: внутренний диаметр трубопровода d = 30 мм; плотность жидкости ρ = 901.6 кг/м 3 ; кинематическая вязкость жидкости ν = 30 мм 2 /с; коэффициент расхода μ = 0.62; толщина стенки трубы δ = 3 мм; F = 5 см 2 – максимальная площадь проходного сечения дросселя; шаг интегрирования Δх = 0.1 м; заданная точность решения итерационного процесса ε = 0.01. В первых трех вариантах расчета динамики потока, связанной с волновыми процессами, практически не наблюдалось, так как τ >> 2 L/c (например, для варианта 3 имеем 2 L/c = 0.03 с < τ = 0.1 с).
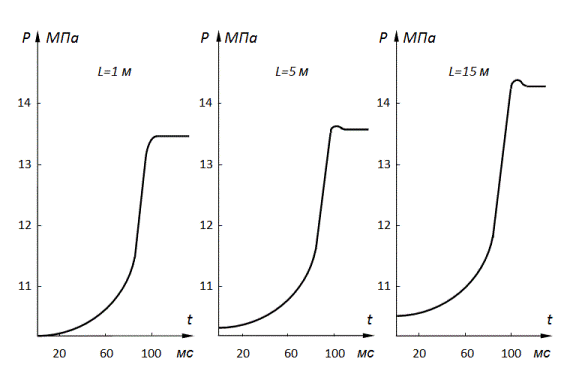
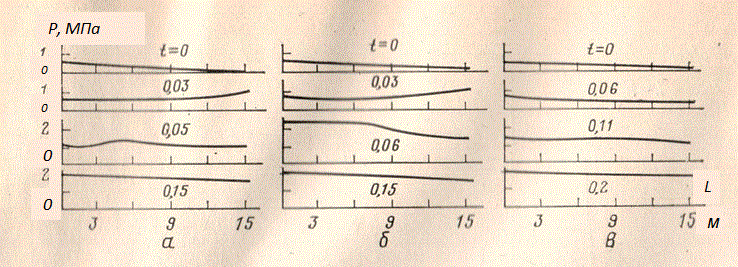
Рис. 8. Динамика давлений на входе трубопроводов при дроссельном регулировании потока на выходе путем изменения площади проходного сечения дросселя по линейному закону На рис.8 приведены графики изменения давлений на входе трубопроводов для указанных трех вариантов модели с распределенными параметрами (18) при дроссельном регулировании потока на выходе (24) путем изменения площади проходного сечения дросселя f ( t ) по линейному закону (22). Рассмотрим распределение давлений по длине трубопровода для вариантов 4–7 (см. табл.). Поскольку длина трубопровода, равная 15 м, может считаться для ряда гидросистем предельной, дальнейшее её увеличение нецелесообразно, поэтому для получения динамики потока за счет волновых процессов, то есть для выполнения условия (25), были рассмотрены варианты 4–6 с пониженными значениями объемного модуля упругости рабочей жидкости Е 1 (490 и 245 Мпа) при перекрытии площади проходного сечения дросселя с F = 5 см 2 до f =1.5 см 2 за время τ = 0.03 с (в варианте 5 τ = 0.1 с). Был также рассмотрен вариант 7 с прежним значением объемного модуля упругости жидкости ( Е 1 = 980 Мпа) и сниженным значением модуля упругости материала трубопровода ( Е 2 = 9.8•10 3 Мпа), характерным для рукавов высокого давления.
Рис. 9. Динамика волновых процессов в трубопроводах с жидкостью Для вариантов 4, 6 и 7 условие (25) выполняется, поэтому должны проявляться волновые процессы, что и было получено в результате расчета (рис.9 а,б ). Величины Е 1 и Е 2 для вариантов 4 и 7 дают одинаковые значения скорости распространения волны, поэтому полученные процессы полностью идентичны (рис.9 б ). Вариант 5 характерен медленным перекрытием дросселя, при котором условие (25) не выполняется, поэтому волновые процессы практически не проявляются (рис.9 в ). Следует отметить, что даже при возникновении волновых процессов последние носят слабо выраженный характер и быстро затухают. Это позволило в свое время сделать вывод, что при динамическом анализе гидросистем, характеризуемых сравнительно короткими участками трубопроводов и относительно малым быстродействием распределительной аппаратуры ( τ ≥ 0.1 с), для описания динамики трубопроводов с жидкостью при дроссельном регулировании приемлема модель с сосредоточенными параметрами без учета инерционной составляющей потока рабочей жидкости. Варьируя различные граничные условия (т.е. вид внешних возмущений на входе и выходе), геометрию и физические параметры трубопроводов и рабочей жидкости, можно еще на стадии проектирования проводить анализ динамических процессов, возникающих в трубопроводах реальных гидросистем. |
Содержание
>> Прикладная математика
>> Численные методы
>> Уравнения математической физики
>> Пример: решение гиперболического уравнения