Алгебраические и трансцендентные уравнения - Метод половинного деления
Метод половинного деления
Рассмотрим уравнение (1):

где функция
F
(
x
) – непрерывна и определена на некотором отрезке
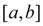 и
и
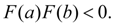
Последнее означает, что функция
F
(
x
) имеет на отрезке
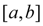 по крайней мере один корень. Рассмотрим случай, когда корень на отрезке
по крайней мере один корень. Рассмотрим случай, когда корень на отрезке
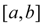 единственный.
единственный.
Делим отрезок пополам. Если
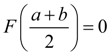 , то
, то
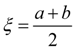 является корнем уравнения (1). Если
является корнем уравнения (1). Если
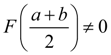 , то рассматриваем ту половину отрезка
, то рассматриваем ту половину отрезка
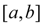 , на концах которой функция
F
(
x
) имеет разные знаки. Новый, более узкий отрезок
, на концах которой функция
F
(
x
) имеет разные знаки. Новый, более узкий отрезок
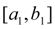 вновь делим пополам и проводим на нем такое же рассмотрение и т.д. В результате на некотором шаге получим либо точное значение корня уравнения (1) , либо последовательность вложенных друг в друга отрезков
вновь делим пополам и проводим на нем такое же рассмотрение и т.д. В результате на некотором шаге получим либо точное значение корня уравнения (1) , либо последовательность вложенных друг в друга отрезков
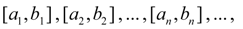 таких, что
таких, что
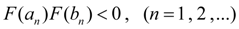 (9)
(9)
и
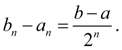 (10)
(10)
Левые концы этих отрезков
 образуют монотонную (неубывающую) ограниченную последовательность, а правые концы
образуют монотонную (неубывающую) ограниченную последовательность, а правые концы
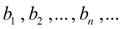 – монотонную (невозрастающую) ограниченную последовательность. Поэтому в силу равенства (10) существует общий предел
– монотонную (невозрастающую) ограниченную последовательность. Поэтому в силу равенства (10) существует общий предел

Переходя в (9) к пределу при
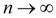 , в силу непрерывности функция
F
(
x
) получим:
, в силу непрерывности функция
F
(
x
) получим:
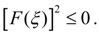 Отсюда
Отсюда
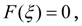 т.е.
т.е.
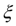 является корнем уравнения (1).
является корнем уравнения (1).
На практике процесс (10) считается завершенным, если
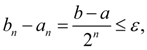 (11)
(11)
где
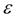 – заданная точность решения.
– заданная точность решения.
|
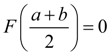 , то
, то
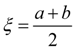 является корнем уравнения (1). Если
является корнем уравнения (1). Если
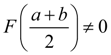 , то рассматриваем ту половину отрезка
, то рассматриваем ту половину отрезка
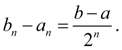 (10)
(10)
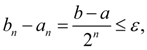 (11)
(11)