Метод касательных (метод Ньютона-Рафсона)Рассмотрим вновь уравнение (1):
где функция
F
(
x
) - дифференцируема и определена на некотором интервале
Разложим функцию F ( x ) в степенной ряд и ограничимся линейной частью разложения:
что эквивалентно замене функции F ( x ) в произвольной точке x ее касательной в этой точке. Тогда из (1) и (5) следует:
Условия сходимости
процесса (8) имеют вид:
1) нулевое приближение
2) вторая производная F ’’ ( x ) не становится слишком большой, 3) первая производная F ’ ( x ) не слишком близка к 0.
Последнее условие означает, что никакие два корня не находятся близко друг от друга, а совместное выполнение условий 2) и 3) аналогично требованию
|
Содержание
>> Прикладная математика
>> Численные методы
>> Алгебраические и трансцендентные yравнения
>> Метод касательных
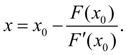 (6)
(6)
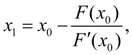 (7)
(7)
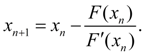 (8)
(8)
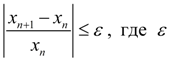 – заданная точность решения.
– заданная точность решения.