Метод итераций (метод последовательных приближений)

Говорят, чтоитерационный процесс сходится , если при выполнении последовательных итераций получаются значения корней, все ближе и ближе приближающиеся к точному значению корня. В противном случае итерационный процесссчитается расходящимся .
Перепишем для удобства уравнение (1) в виде:

(3)

что можно получить путем замены: .
Пусть – нулевое приближение, т.е. начальное приближенное значение корня уравнения (3). Тогда в качестве следующего, 1-го, приближения примем

следующим, 2-м, приближением будет

и т.д.,  в качестве n -го приближения примем

(4)

Здесь возникает главный вопрос: приближается ли к истинному решению уравнения (3) при неограниченном возрастании n ? Иными словами, сходится ли итерационный процесс (4) ?

Уловия сходимости метода итераций [2]: если при всех значениях , вычисляемых в процессе (4) решения задачи:
1) , то итерационный процесс сходится;
2) , то итерационный процесс расходится.

Если производная в некоторых точках по модулю меньше 1, а в других точках – больше 1, то ничего определенного о сходимости итерационного процесса сказать нельзя. Он может как сходиться, так и расходиться.

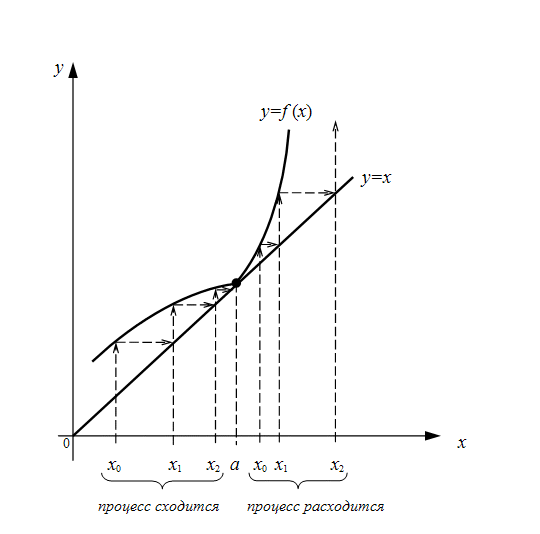
Если итерационный процесс расходится, то причиной этого часто является неудачный выбор нулевого приближения. Так, на рис. 1 показано, что выбор нулевого приближения существенно влияет на сходимость итерационного процесса. Это напрямую связано с тем, находится ли нулевое приближение в области, где выполняются условия сходимости итерационного процесса.

Рис. 1. Зависимость сходимости итерационного процесса от выбора нулевого приближения

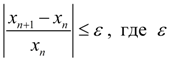Процесс (4) считается завершенным, если – заданная точность решения.