Алгоритмы формирования и решения математической модели схемы
Формирование исходных данных.
Вся исходная информация для проведения динамического анализа состоит из двух частей:
Первая часть исходной информации строится в соответствии с изложенным выше методом структурного описания гидросхем , основанном на классификации базовых гидроэлементов, введении обобщенного линейного динамического ЗВЕНА с узлами i (вход), j (выход) и k (дополнительный вход для звена – сумматора). На основании этого каждое динамическое звено получило идентификатор е (ЗВЕНО) и код, однозначно определяющий группу уравнений для математического описания звена данного типа. В соответствии с этим разработана специальная таблица для задания исходных данных исходных данных динамических звеньев, имеющая следующую структуру:
где
n
– номер звена;
А
– матрица-строка коэффициентов, характеризующих физические, геометрические и конструктивные параметры звена, что составляет содержание второй части исходной информации.
Формирование математической модели системы управления. В результате анализа строки таблицы исходных данных (6) для каждого динамического звена в зависимости от его типа строится система дифференциальных и/или алгебраических уравнений вида:
где
Матрица связей:
Матрица параметров элементов гидросистемы:
Формирование математической модели системы управления
осуществляется следующим образом.
Рассматривается звено
Внешние возмущения и сигналы управления. Управление моделью (решением системы уравнений) осуществляется специальным блоком, в функцию которого входит генерирование сигналов внешнего воздействия. В блоке управления можно смоделировать как типовые внешние возмущения (синусоидальное, скачкообразное, линейное и т.п.), так и нестандартные, имеющие место в большинстве случаев и определяемые конкретной задачей. Более того, для рассмотрения задач с изменяющимися физическими и конструктивными параметрами в блоке управления можно предусмотреть задание этих величин в функции времени или другой переменной, получаемой в результате решения. Кроме того, в блоке управления представляется возможным задание управляющих воздействий и сил сопротивления как функций, аппроксимируемых конечным набором дискретных значений или имеющих определенный спектр. Алгоритм решения. Для интегрирования систем дифференциальных уравнений в настоящее время существует огромное количество методов численного интегрирования (методы Рунге-Кутта, Эйлера и их модификации, метод Гира и т.д.), на базе которых разработано множество различных программ, что позволяет всегда выбрать подходящий аппарат решения. |
Содержание
>> Инженерная математика
>> Системы управления
>> Динамический анализ системы управления объемным гидроприводом
>> Алгоритмы формирования и решения математической модели схемы
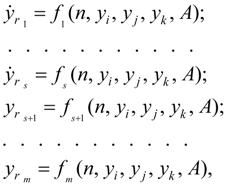 (7)
(7)
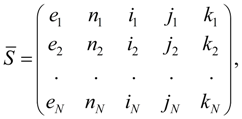 (8)
(8)
 (9)
(9)