Библиотека математических моделей типовых линейных динамических звеньев
В системах управления
используются разнообразные физические устройства: гидравлические, электромагнитные, электрогидравлические и др. Поэтому при решении задач динамики систем приходится моделировать различные по своей природе системы управления и регулирования. Большинство из них хорошо описывается с помощью типовых линейных динамических звеньев автоматического регулирования [1], к которым относятся:
1) идеальное усилительное (безынерционное) звено – сумматор;
2) апериодическое звено 1-го порядка (инерционное);
3) апериодическое звено 2-го порядка;
4) колебательное звено;
4
a
) консервативное звено (частный случай колебательного звена);
5) идеальное интегрирующее звено;
6) инерциальное интегрирующее звено;
7) идеальное дифференцирующее звено;
8) идеальное звено с введением производной;
9) инерционное дифференцирующее звено;
10) динамическое звено 2-го порядка (общий случай).
Математические модели перечисленных линейных динамических звеньев записаны далее в виде обыкновенных дифференциальных уравнений, а не в операторной форме (в виде передаточных функций), поскольку нас интересуют переходные процессы во временно’й, а не в частотной области. В общем случае линейное динамическое звено 2-го порядка описывается уравнением:
где
Для всех остальных типов динамических звеньев их уравнения получены как частные случаи (2):
идеальное усилительное (безынерционное) звено – сумматор:
апериодическое звено 1-го порядка (инерционное):
апериодическое звено 2-го порядка и колебательное звено:
консервативное звено:
идеальное интегрирующее звено:
инерциальное интегрирующее звено:
идеальное дифференцирующее звено:
идеальное звено с введением производной:
инерционное дифференцирующее звено:
Таким образом, все типовые линейные звенья могут быть объединены в один обобщенный элемент ЗВЕНО (идентификатор этого элемента в библиотеке базовых элементов) с узлами
i
(вход),
j
(выход),
k
(дополнительный вход для звена – сумматора).
Условия, ограничения, комментарии. Приведенные уравнения линейных динамических звеньев следует дополнить рядом ограничений, отражающих физические свойства переменных, а также некоторые конструктивные особенности устройств (например, упоры подвижных частей). В ряде реальных элементов перемещение z подвижных частей ограничено упорами. Такого рода нелинейности могут быть заданы в виде неравенств:
|
Содержание
>> Инженерная математика
>> Системы управления
>> Динамический анализ системы управления объемным гидроприводом
>> Библиотека математических моделей типовых динамических звеньев
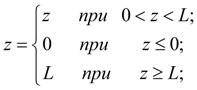 (3)
(3)
 (4)
(4)
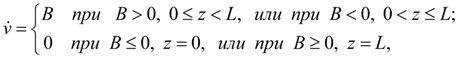 (5)
(5)