Случайные величины и законы распределенияПеременная величина называется случайной , если в результате опыта она может принимать действительные значения с определёнными вероятностями. Наиболее полной, исчерпывающей характеристикой случайной величины является закон распределения. Закон распределения – функция (таблица, график, формула), позволяющая определять вероятность того, что случайная величина Х принимает определеное значение х i или попадает в некоторый интервал. Если случайная величина имеет данный закон распределения, то говорят, что она распределена по этому закону или подчиняется этому закону распределения. Случайная величина Х называется дискретной , если существует такая неотрицательная функция
которая ставит в соответствие значению
х
i
переменной
Х
вероятность
р
i
, с которой она принимает это значение.
Случайная величина Х называется непрерывной , если для любых a < b существует такая неотрицательная функция f ( x ), что
Функция
f
(
x
) называется
плотностью распределения
непрерывной случайной величины.
Вероятность того, что случайная величина Х (дискретная или непрерывная) принимает значение, меньшее х , называется функцией распределения случайной величины Х и обозначается F ( x ) :
Функция распределения является универсальным видом закона распределения, пригодным для любой случайной величины. Общие свойства функции распределения:
Кроме этого универсального, существуют также частные виды законов распределения:
ряд распределения
Основные свойства плотности распределения:
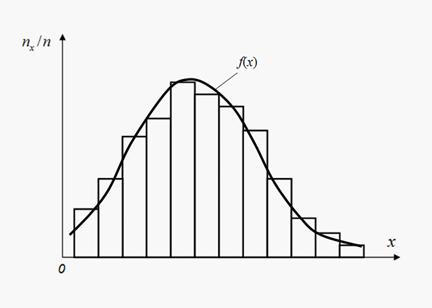
Рис. 1. Гистограмма и выравнивающая плотность распределения
Однако, часто бывает достаточно указать только отдельные числовые параметры, характеризующие основные свойства распределения. Эти числа называются числовыми характеристиками случайной величины. |
Содержание
>> Прикладная математика
>> Математическая статистика
>> Элементы математической статистики
>> Случайные величины и законы распределения
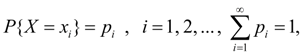 (1)
(1)
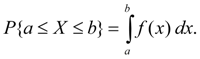 (2)
(2)
 (4)
(4)
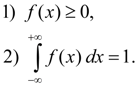 (5)
(5)