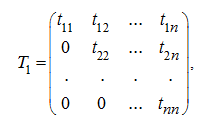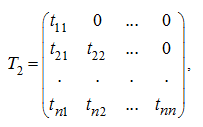|
Матричная алгебра - Треугольные матрицы
Треугольные матрицы
Квадратная матрица называется
треугольной
, если ее элементы, стоящие выше (ниже) главной диагонали, равны нулю. Например, матрица
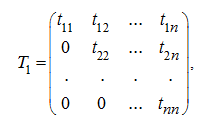
где
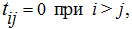 является
верхней треугольной
матрицей
, а матрица
является
верхней треугольной
матрицей
, а матрица
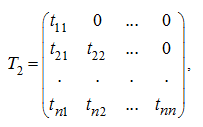
где
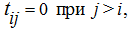 является
нижней треугольной матрицей
.
является
нижней треугольной матрицей
.
Диагональная матрица является частным случаем треугольной матрицы (как верхней, так и нижней). Очевидно, что
определитель треугольной матрицы равен произведению ее диагональных элементов
, то есть в наших примерах:
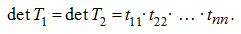
Поэтому треугольная матрица является невырожденной тогда и только тогда, когда все ее диагональные элементы отличны от нуля.
Сумма и произведение треугольных матриц одной и той же размерности и одинаковой структуры (то есть, обе – верхние, или обе – нижние) являются также треугольными матрицами той же размерности и структуры.
Обратная матрица невырожденной треугольной матрицы – также треугольная матрица той же размерности и структуры. Исходя из этого, обращение треугольной матрицы не вызывает никаких затруднений.
|