Регрессионный анализ. Метод наименьших квадратов
Одной из часто встречающихся задач при обработке результатов эксперимента является подбор формулы для установления функциональной зависимости между экспериментальными данными, так называемого
уравнения регрессии
. Прежде чем приступить к подбору формулы, целесообразно нанести опытные данные на график и на глаз, от руки провести через полученные точки наиболее правдоподобную кривую. Очень часто общий вид кривой бывает известен из других соображений, что упрощает задачу, сводя ее к поиску числовых коэффициентов известной функциональной зависимости общего вида (например, прямолинейной, квадратичной, логарифмической и др.). При этом часто становятся видны те опытные данные, которые скорее всего содержат наибольшие погрешности. Кроме полученных экспериментальных точек существенным моментом при проведении кривой являются соображения общего характера: как ведет себя кривая вблизи нуля, пересекает ли она координатные оси, касается ли их, имеет ли асимптоты и т.д.
После того, как эта предварительная работа проделана, начинается собственно подбор формулы – уравнения регрессии. Решением задач, связанных с поиском уравнений регрессии занимается
регрессионный анализ
, а одним из его наиболее широко применяемых на практике алгоритмов является
метод наименьших квадратов
[ 3, 5, 6, 7].
В общем случае задача метода наименьших квадратов формулируется следующим образом. Пусть искомая функциональная зависимость величины у от величины х выражается формулой:
где
Метод наименьших квадратов
состоит в том, что
оценки параметров
достигает наименьшего значения .
Для определения этих оценок нужно продифференцировать (2) по всем оценкам
Система уравнений (3) называется системой нормальных уравнений Гаусса . Здесь для краткости записи приняты следующие обозначения сумм:
|
Содержание
>> Прикладная математика
>> Математическая статистика
>> Обработка результатов эксперимента
>> Регрессионный анализ. Метод наименьших квадратов
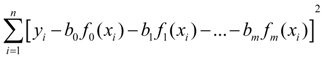 (2)
(2)
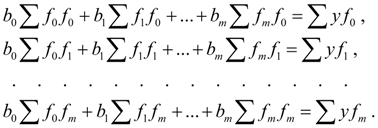 (3)
(3)
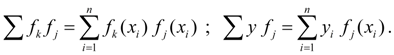 (4)
(4)